记得高中很讨厌政治课，但是有几个词烙在脑子里，想忘都忘不掉，比如“世界观”和“方法论”，当时那位老爷爷整天给我们灌输这些玩意儿，搞得我现在对这些词汇仍然如鬼神般敬而远之。这次我要写的是关于统计方法的一些思考（主要是思路），但又不太多涉及方法本身的推导证明，因此只好称之为“方法观”。

现在每天感慨统计领域太宽，模型太多，方法太杂，让人把握不住方向。不过上次高校研究生统计论坛我仍然不知天高地厚地选了一个讲述统计思想的题目，其原因正是觉得方法太杂，应该理出一些头绪来；当然我所理的头绪也仅仅是很局部（local）的，管中窥豹而已。下面我先举几个例子说明一些统计方法的发展思路，这些也是我在上次论坛上发言的部分内容：

一、纵向数据与空间统计学

纵向数据（Longitudinal Data）和空间统计学（Spatial Statistics）算是代表了统计学发展领域的两个前进维度；众所周知，统计的数据有截面数据（Cross-section）和时间序列数据（Time-series）之分，前者是在同一时点观测不同个体得到的数据，后者是在不同时点观测同一个个体（当然也可以不同）得到的，这两种数据都有比较成熟的分析方法，如回归、多元、ARMA等等，而纵向数据则可视作是它们的“综合”：对不同的个体在不同的时点上（重复）观测——这体现的是时间的维度；而空间统计学则是结合地理学的知识，运用统计分析方法去分析与地理相关的问题，这里我摘一段Wikipedia 中关于空间统计学的介绍：

“Applications within GIS; mathematical analysis on varied spatial datasets; Issues on human geography, particularly those involving the spread of disease (epidemiology), the practice of commerce and military planning (logistics), and the development of efficient spatial networks.” …

其中GIS是地理信息系统，也是现在研究应用比较火热的技术；空间统计学牵涉的领域有疾病的散布（流行病学）、商业和军事规划（后勤）以及开发有效的空间网络等等。听起来挺有意思。此外，一些传统的统计学概念、模型也被自然而然的转移到空间统计学中，比如空间回归（Spatial Regression）、空间滞后模型（Spatial Lagged）、空间自相关（Autocorrelation）、空间计量经济学（Spatial Econometrics）等。

若对R有所了解，不妨看看相应的一些Package，对于纵向数据，一般使用nlme（John Fox 的文档 ）；对于空间统计学，可以参见相应的Task View。

二、分位数回归与均值回归

众所周知，经典的最小二乘回归是针对因变量的均值（期望）的：模型反映了因变量的均值怎样受自变量的影响——\(y=X\beta+\epsilon\)，\(E(y)=X\beta\)；这个小小的式子说明了经典回归的本质，自变量（有时也称为协变量Covariates）影响着因变量的一个位置参数量，从这个意义上，可以把回归称之为一个位置移动模型（Location Shift Model）；用最小二乘方法容易推出，使\(\sum_{i}(y_i-\xi)^2\)最小的\(\xi\)正是\(\xi=\bar{y}\)。

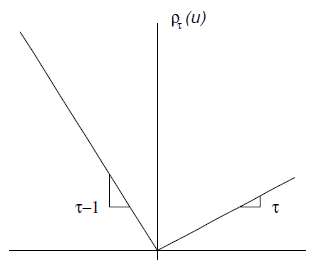
分位数回归（Quantile Regression）的核心思想就是从这个Location的角度出发而产生的，把Location从均值推广到分位数，回归家族也就增添了分位数回归这位新成员。最小二乘回归的目标是最小化误差平方和，分位数回归也是最小化一个新的目标函数：

$$\min_{\xi \in \mathcal{R}} \sum \rho_{\tau}(y_i-\xi)$$

同样我们可以看看什么样的\(\xi\)使得上面的目标函数最小？通过对\(\xi\)简单的求导，不难发现满足条件的\(\xi\)正是\(y\)的\(\tau\)分位数 。

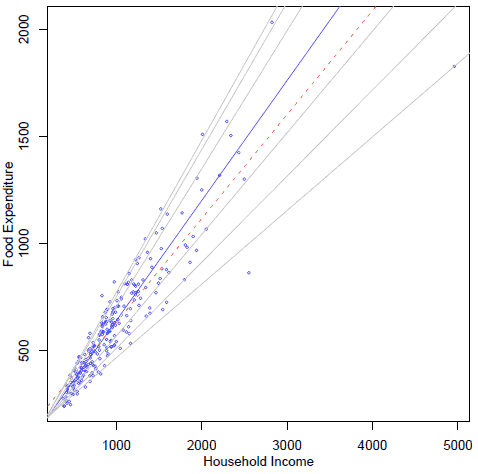
在R中，与分位数回归对应的包是quantreg，这个包也有自带的一份Vignette，对于分位数回归的学习者来说绝对是好材料（位于/doc目录下，rq.pdf）。这份文档中举了一个关于恩格尔系数的例子（见图 2），图中虚线是最小二乘回归结果，黑线是中位数回归结果（实际上就是\(\tau=0.5\)），灰线从下至上分别是0.05、0.1、0.25、0.75、 0.90、0.95分位数；从图中可以看出，大趋势是随家庭收入增大，食品支出也增加（废话！），但是在给定家庭收入的情况下，食品支出的不同分位数的变化趋势（斜率）是有差别的，高分位变化更陡峭，而低分位相对平缓；说明的实际问题大约也就是恩格尔系数高的家庭更倾向于在食品上花钱。相比起来，最小二乘回归就不能说明这样的趋势，而只能说明前面那句“废话”。

三、Bootstrap & Jackknife 与抽样

在统计的世界，我们面临的总是只有样本，Where there is sample, there is uncertainty，正因为不确定性的存在，才使统计能够生生不息。传说统计学家、数学家和物理学家乘坐一列火车上旅行，路上看到草原上有一只黑羊，统计学家说，“基于这个样本来看，这片草原上所有的羊都是黑的”，数学家说，“只有眼前这只羊是黑的”，物理学家则说，“你们都不对，只有羊的这一面是黑的”。这是关于统计和其他学科的一个玩笑话，说明了统计的一些特征，比如基于样本推断总体。

一般情况下，总体永远都无法知道，我们能利用的只有样本，现在的问题是，样本该怎样利用呢？Bootstrap的奥义也就是：既然样本是抽出来的，那我何不从样本中再抽样（Resample）？Jackknife的奥义在于：既然样本是抽出来的，那我在作估计、推断的时候“扔掉”几个样本点看看效果如何？既然人们要质疑估计的稳定性，那么我们就用样本的样本去证明吧。

John Fox的那一系列附录中有一篇叫“Bootstrapping Regression Models”，当我看到第二页用方框框标出那句话时，我才对Bootstrap的思想真正有了了解（之前迷茫了很长时间）。Bootstrap的一般的抽样方式都是“有放回地全抽”（其实样本量也要视情况而定，不一定非要与原样本量相等），意思就是抽取的Bootstrap样本量与原样本相同，只是在抽样方式上采取有放回地抽，这样的抽样可以进行B次，每次都可以求一个相应的统计量/估计量，最后看看这个统计量的稳定性如何（用方差表示）。Jackknife的抽样痕迹不明显，但主旨也是取样本的样本，在作估计推断时，每次先排除一个或者多个样本点，然后用剩下的样本点求一个相应的统计量，最后也可以看统计量的稳定性如何。

在R中简单随机抽样的函数是sample()，其中有个参数replacement表示是否放回，经典的抽样基本都是不放回（replace = FALSE），而Bootstrap则是replace = TRUE；从FALSE到TRUE，小小的一个变化，孕育了Bootstrap的经典思想。

结语：例子暂举这么三个，对于一些大思想，我（不知天高地厚地）尽力以一句话概括出来，看似简单，其实里面的工作还很多，Quantile Regression的老大Roger Koenker等、Bootstrap的老大Efron等都有相应的著作，闲着没事干的同学不妨翻翻，不过我个人并不推荐这种方式，原因是看英文著作太花时间，最好先找点介绍性的材料看看，心里有把握之后再去找详细的材料翻阅。

平时学习中我比较注重研究统计模型和方法，但是对于理论性的东西我也有我的看法，到现在为止，我对模型的评判标准可以总结为：

1. 其目的能用一句话概括，或者结果能用图形直观展示；（目标）
2. 数学公式能对应上某种成熟的生活观念。（手段）

如果模型不符合这两条标准，我是不愿花功夫研究学习的。虽然在一定程度上追求模型的“先进性”，但是骨子里仍然认为统计应该与实际有紧密联系，否则统计也没什么存在的价值。所以概括起来，我追求的目标仍然是一个映射（Mapping）：从理论到实践。

对于统计的理论方法，我一般看两个问题，与上面的标准对应：目标是什么？手段是什么（数学公式是否能与实际对应）？比如对于回归，目标：寻找自变量和因变量之间尽可能精确的（线性或非线性）关系；手段：使误差平方和最小，而误差平方和说明的是什么？就是因变量的期望值与实际值的差距，由于因变量的期望是通过自变量来计算的，因此从实际来看，这里的“差距 ”越小也就说明自变量与因变量之间的关系越精确——正好与前面的目标对应。类似还能总结出其它例子，比如现在国内应用如火如荼的结构方程模型（Sturctural Equation Model，SEM）——目标：寻找观测变量和潜变量之间尽可能精确的关系；手段：最小化样本协方差阵与理论协方差阵之间的差距。若我们要对统计方法提出质疑，则可以直接从其数学手段切入，比如“最小化样本协方差阵与理论协方差阵之间的差距”是否能保证找出观测变量和潜变量之间的精确关系？把理论和实际的差距转化为协方差阵的差距，这一点从直观上太难想象，不像回归那样，就是两个数字作减法说明差距。因此，我对SEM一直是雾里看花，有些“朦胧感”，这也是我对SEM持保留态度的原因之一，本质就在于我难以构建一个从理论到实际的“映射”。

最后再谈一点关于建模的想法。

关于统计建模，我一向坚持以“简洁而能说明问题”为首要原则，并且更强调“简洁”；事实上，知道赤池信息量的人都知道，AIC（Akaike Information Criterion）的计算是两部分之和，一部分是（-2倍的）对数似然函数最大值，另一部分就是（2倍的）模型未知参数个数，“使AIC尽可能小”是一条著名的统计建模准则，显然，第二部分说的无非就是模型的简洁程度。我反对一味追求数学上的复杂与高深，搞统计不是比谁的数学更拽，要是脱离实际或者对实际没有指导作用，那么模型再花哨、方法再先进也不过是个绣花枕头——中看不中用。

曾经有人问我认为什么统计方法最好，我不假思索地回答，“‘散点图’呗！”当然，这里面也有开玩笑的成份，但意思也是想表达统计方法的应用，应该能让人家容易理解你的意图。“文章合为时而著，歌诗合为事而作。”那么，统计为谁而做？大家不妨自行思考吧。

本文写于2007-01-27