用GeoBUGS做简单的空间数据分析

第一节 实例介绍基本的空间模型

GeoBUGS是WinBUGS的一个模块，专门用来分析空间数据（spatial data)。由于和WinBUGS的基本模型结合得比较好，所以被广泛地使用。目前的GeoBUGS除了自身的地图格式外，还支持Splus, ArcInfo 以及 EpiMap的地图格式。当然了，在使用的时候需要做适当的转化才行。

下面是一个简单的例子，大家也可以在GeoBUGS的Manual中找到它。模型假设为条件自回归模型 Conditional Autoregressive（CAR）。数据为苏格兰唇癌疾病数据，反映的是苏格兰56个郡的唇癌发病率。这个数据比较经典，Clayton and Kaldor (1987) 和 Breslow and Clayton (1993)都曾在他们的论著中分析过该数据。

County	Observed	Expected	Percentage	SMR	Adjacent
	cases (Oi)	cases (Ei)	in agric.(xi)		counties
1 	9 		1.4 		16 		652.2 	5,9,11,19
2 	39 		8.7 		16 		450.3 	7,10
… 	… 		… 		… 		… 	…
56 	0 		1.8 		10 		0.0 	18,24,30,33,45,55

County 为郡的编号。

Observed cases（记作：Oi）为实际患病人数。

Expected cases（记作：Ei）为预计患病人数，这个人数基于当地的人口，对象的年龄、性别分布。

Percentage in agric.（记作：xi）为当地农业、渔业、林业人口所占当地总人口的比例。

Adjacent counties 指的是与当前郡相毗邻的郡的编号。

SMR（Standardised Mortality Ratios）为标准死亡率。

通过观察数据，我们可以发现SMR在某些时候（比如Oi和Ei较小时）出现奇异的值（如 0.0），所以我们需要通过smooth方法来调整SMR的值。这里我们采用的方法是在条件自相关（CAR）的先验假定下，拟合具有空间相关的随机混效Poisson模型。模型如下：

$$O_i \sim Poisson (\mu_i) $$

$$log \mu_i = log E_i + \alpha_0 + \alpha_1 x_i / 10 + b_i$$

其中$\alpha_0$为intercept项反映的是各个区域间患病的相对基准风险。

$b_i$反映的是与地域相关的潜在的患病风险因子。其他项不言自明。

需要重点提出的是这里的$b_i$,在GeoBUGS中可以通过car.normal先验分布来描述。在贝叶斯统计中任河变量都可以通过一个分布来描述。

b[1:N] ~ car.normal(adj[], weights[], num[], tau)

adj[] 为邻接郡的编号

weights[] 为描述各个郡之间重要性差异的权因子

num[] 每个郡的相邻郡的个数

tau 反映的是精度，因为不知道，所以在模型设定时要将其放到先验参数中去。

通过前两次介绍的方法，我们很容易就可以得到模型的结果。下面我们来看看如何将结果反映到地图上去。

第二节 GeoBUGS的界面操作

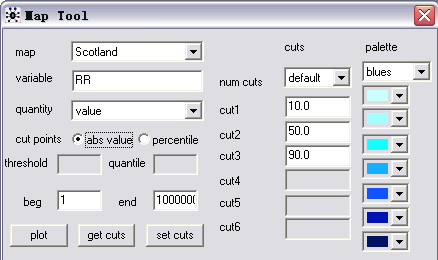
GeoBUGS的地图工具配置界面

第一步，打开Map-> Map Tool菜单，选择Scotland这张地图

第二步，在variable中填O或者E或者b等等模型参数

第三步，设置分割点和地图模板

第四步，点击plot画图

当然还可以在quantity中设置不同的需要反映的量的类型。

很简单吧。

GeoBUGS生成的地图

GeoBUGS还提供了一些小工具，比如Adjacency Map来查看邻接图。

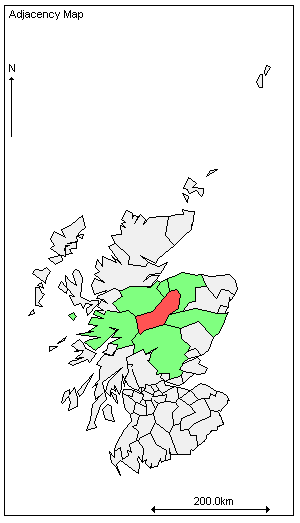
用GeoBUGS显示邻接地图

附录

以下是WinBUGS用到的模型代码：

#Model
model
{
    for (i in 1:N) {
        O[i] ~ dpois(mu[i])
        log(mu[i]) <- log(E[i]) + alpha0 + alpha1 * X[i]/10 +
            b[i]
        RR[i] <- exp(alpha0 + alpha1 * X[i]/10 + b[i])
        # Area-specific relative risk (for maps)
    }
    # CAR prior distribution for random effects:
    b[1:N] ~ car.normal(adj[], weights[], num[], tau)
    for (k in 1:sumNumNeigh) {
        weights[k] <- 1
    }
    # Other priors:
    alpha0 ~ dflat()
    alpha1 ~ dnorm(0, 1e-05)
    tau ~ dgamma(0.5, 5e-04)
    # prior on precision
    sigma <- sqrt(1/tau)
    # standard deviation
}
#Data
list(N = 56, O = c(9, 39, 11, 9, 15, 8, 26, 7, 6,
    20, 13, 5, 3, 8, 17, 9, 2, 7, 9, 7, 16, 31, 11, 7, 19, 15,
    7, 10, 16, 11, 5, 3, 7, 8, 11, 9, 11, 8, 6, 4, 10, 8, 2,
    6, 19, 3, 2, 3, 28, 6, 1, 1, 1, 1, 0, 0), E = c(1.4, 8.7,
    3, 2.5, 4.3, 2.4, 8.1, 2.3, 2, 6.6, 4.4, 1.8, 1.1, 3.3, 7.8,
    4.6, 1.1, 4.2, 5.5, 4.4, 10.5, 22.7, 8.8, 5.6, 15.5, 12.5,
    6, 9, 14.4, 10.2, 4.8, 2.9, 7, 8.5, 12.3, 10.1, 12.7, 9.4,
    7.2, 5.3, 18.8, 15.8, 4.3, 14.6, 50.7, 8.2, 5.6, 9.3, 88.7,
    19.6, 3.4, 3.6, 5.7, 7, 4.2, 1.8), X = c(16, 16, 10, 24,
    10, 24, 10, 7, 7, 16, 7, 16, 10, 24, 7, 16, 10, 7, 7, 10,
    7, 16, 10, 7, 1, 1, 7, 7, 10, 10, 7, 24, 10, 7, 7, 0, 10,
    1, 16, 0, 1, 16, 16, 0, 1, 7, 1, 1, 0, 1, 1, 0, 1, 1, 16,
    10), num = c(3, 2, 1, 3, 3, 0, 5, 0, 5, 4, 0, 2, 3, 3, 2,
    6, 6, 6, 5, 3, 3, 2, 4, 8, 3, 3, 4, 4, 11, 6, 7, 3, 4, 9,
    4, 2, 4, 6, 3, 4, 5, 5, 4, 5, 4, 6, 6, 4, 9, 2, 4, 4, 4,
    5, 6, 5), adj = c(19, 9, 5, 10, 7, 12, 28, 20, 18, 19, 12,
    1, 17, 16, 13, 10, 2, 29, 23, 19, 17, 1, 22, 16, 7, 2, 5,
    3, 19, 17, 7, 35, 32, 31, 29, 25, 29, 22, 21, 17, 10, 7,
    29, 19, 16, 13, 9, 7, 56, 55, 33, 28, 20, 4, 17, 13, 9, 5,
    1, 56, 18, 4, 50, 29, 16, 16, 10, 39, 34, 29, 9, 56, 55,
    48, 47, 44, 31, 30, 27, 29, 26, 15, 43, 29, 25, 56, 32, 31,
    24, 45, 33, 18, 4, 50, 43, 34, 26, 25, 23, 21, 17, 16, 15,
    9, 55, 45, 44, 42, 38, 24, 47, 46, 35, 32, 27, 24, 14, 31,
    27, 14, 55, 45, 28, 18, 54, 52, 51, 43, 42, 40, 39, 29, 23,
    46, 37, 31, 14, 41, 37, 46, 41, 36, 35, 54, 51, 49, 44, 42,
    30, 40, 34, 23, 52, 49, 39, 34, 53, 49, 46, 37, 36, 51, 43,
    38, 34, 30, 42, 34, 29, 26, 49, 48, 38, 30, 24, 55, 33, 30,
    28, 53, 47, 41, 37, 35, 31, 53, 49, 48, 46, 31, 24, 49, 47,
    44, 24, 54, 53, 52, 48, 47, 44, 41, 40, 38, 29, 21, 54, 42,
    38, 34, 54, 49, 40, 34, 49, 47, 46, 41, 52, 51, 49, 38, 34,
    56, 45, 33, 30, 24, 18, 55, 27, 24, 20, 18), sumNumNeigh = 234)
#Inits
list(tau = 1, alpha0 = 0, alpha1 = 0, b = c(0, 0,
    0, 0, 0, NA, 0, NA, 0, 0, NA, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0))

WinBUGS在统计分析中的应用 第三部分完