一、一个例子

核密度估计应该是大家常用的一种非参数密度估计方法，从某种程度上来说它的性质比直方图更好，可以替代直方图来展示数据的密度分布。但是相信大家会经常遇到一个问题，那就是有些数据是严格大于或等于零的，在这种情况下，零附近的密度估计往往会出现不理想的情况。下面以一个指数分布的模拟数据为例（样本量为1000），R程序代码为：

set.seed(123)
x <- rexp(1000, 1)
plot(density(x, kernel = "epanechnikov"), ylim = c(0, 1.2))
lines(seq(0, 8, by = 0.02), dexp(seq(0, 8, by = 0.02), 1), col = "blue")
abline(v = 0, col = "red")

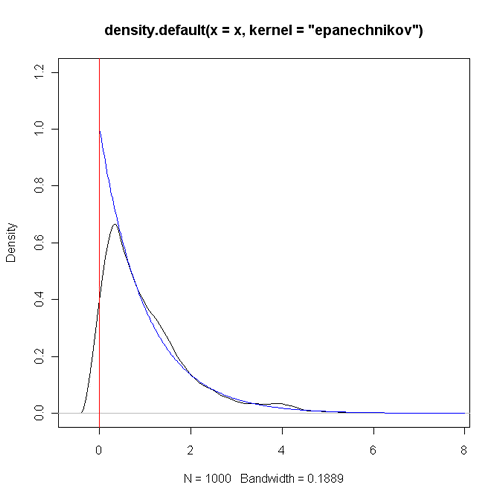
可以看出，理论上应该单调递减的密度函数在0附近有明显的“陡坡”，而且不应该有密度的小于零的区域也有着正的估计值。当样本量增大时，这种现象也不会得到明显好转，下图是将样本量改为10000时的情形。

set.seed(123)
x <- rexp(10000, 1)
plot(density(x, kernel = "epanechnikov"), ylim = c(0, 1.2))
lines(seq(0, 8, by = 0.02), dexp(seq(0, 8, by = 0.02), 1), col = "blue")
abline(v = 0, col = "red")

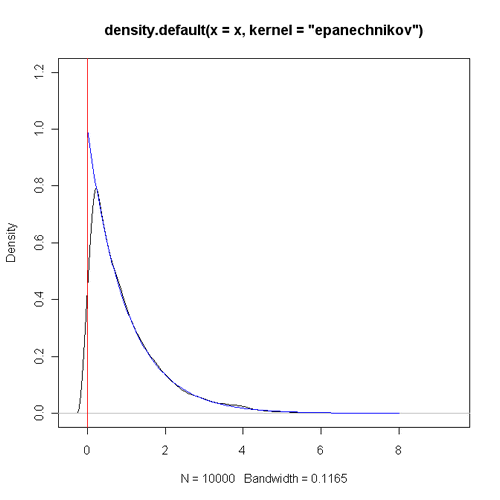
我们也许从平时看的书中了解到，当样本量趋于无穷时，核密度估计值将是收敛到真实的密度函数的，但我们可能不会特意去研究那些结论成立的条件。以上这两个简单的例子似乎给了我们一个直观的感觉，那就是当真实密度函数的支撑集（函数$f(x)$的支撑集指的是使得$f(x)\neq 0$的x的集合）有边界时，核密度估计值可能会出现一些不理想的情况。下面就简单地给出一些理论的结果。

二、理论分析

在一些必要的条件下（真实的密度函数$f$二阶导绝对连续，三阶导平方可积），核密度估计值\(\hat{f}(x)\)的偏差有表达式\(Bias[\hat{f}(x)]=\frac{h^2\sigma_k^2f''(x)}{2}+O(h^4)\)，其中$h$是带宽，\(\sigma_k^2=\int u^2k(u)du\)，$k(u)$是支集为$[-1,1]$的核函数（即在$[-1,1]$上有值，其余的地方取零）。可以看出这个偏差是随着带宽$h$的减小以\(h^2\)的速度趋于零的。

而假设密度函数以0为边界，那么上述表达式将不再成立，而是代之以

$$E[\hat{f}_k(x)]=a_0(x)f(x)-ha_1(x)f'(x)+O(h^2)$$

其中\(a_i(x)=\int_{-1}^{x/h}u^ik(u)du\)。可以看出，当\(x \ge h\)时，\(a_0(x)=1\)，\(a_1(x)=0\)，此时的偏差跟之前的那个表达式没有区别；但当\(0 \le x<h\)时，\(a_0(x)\)和\(a_1(x)\)都是非零的，于是偏差总是存在。

也许你会提议说，将估计值除以\(a_0(x)\)，偏差就可以减小了吧？的确，这样是一种改进的办法，但也要注意到，此时$h$的一次项不会消除，也就是说原来\(h^2\)的衰减速度放慢到了$h$，从效率上说相对于理想的情况是大打了折扣。

这时候一个巧妙的办法是，用另外一个核函数$l(x)$对f也做一次估计，那么就有

$$E[\hat{f}_l(x)]=b_0(x)f(x)-hb_1(x)f'(x)+O(h^2)$$

其中的\(b_0\)和\(b_1\)意义类似，只不过是针对$l(x)$的。

对以上两个式子进行线性组合，则会有

$$b_1(x)*E[\hat{f}_k(x)]-a_1(x)*E[\hat{f}_l(x)]=[b_1(x)a_0(x)-a_1(x)b_0(x)]f(x)+O(h^2)$$

然后把$f(x)$的系数移到等式左边，$O(h)$项的偏差就神奇地消失了。

通过观察核密度估计的表达式，我们可以将上面这个过程等价地认为是对$f(x)$用了一个新的核函数进行估计，这个新的核函数是

$$p(x)=\frac{b_1(x)k(x)-a_1(x)l(x)}{b_1(x)a_0(x)-a_1(x)b_0(x)}$$

特别地，如果将$l(x)$取为$x*k(x)$，那么$p(x)$将有一个简单的形式

$$p(x)=\frac{(a_2(x)-a_1(x)x)k(x)}{a_0(x)a_2(x)-a_1^2(x)}$$

当\(x \ge h\)时，这个新的核函数$p(x)$就是$k(x)$，而当\(x \ge h\)时（也就是在边界），它会对最初的核函数进行调整。当\(x<0\)时，不管算出来的估计值是多少，都只需将密度的估计值取为0即可。

三、程序实现

下面这段程序是对本文的第一幅图进行“整容”，代码及效果图如下：

k <- function(x) 3 / 4 * (1 - x^2) * (abs(x) <= 1)
a0 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  0.75 * (ub - lb) - 0.25 * (ub^3 - lb^3)
}
a1 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  3 / 8 * (ub^2 - lb^2) - 3 / 16 * (ub^4 - lb^4)
}
a2 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  0.25 * (ub^3 - lb^3) - 0.15 * (ub^5 - lb^5)
}
kernel.new <- function(x, u, h) {
  k(x) * (a2(u, h) - a1(u, h) * x) / (a0(u, h) * a2(u, h) - a1(u, h)^2)
}
den.est <- function(u, ui, h) {
  sapply(u, function(u) ifelse(u < 0, 0, mean(kernel.new((u - ui) / h, u, h)) / h))
}
set.seed(123)
dat <- rexp(1000, 1)
x <- seq(0, 8, by = 0.02)
y <- den.est(x, dat, 2 * bw.nrd0(dat))
plot(x, y, type = "l", ylim = c(0, 1.2), main = "Corrected Kernel")
lines(x, dexp(x, 1), col = "red")

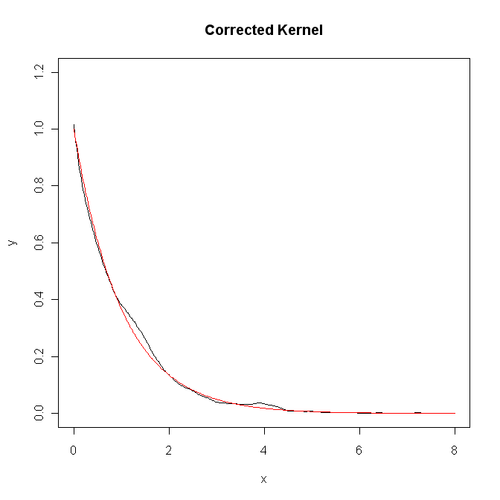
从中可以看出，边界的偏差问题已经得到了很好的改进。

如果真实的密度函数的支集不是$[0,+∞]$，而是某一个闭区间$[m,n]$，那么偏差修正的过程与上面类似，只不过是要将\(a_i(x)\)定义为\(a_i(x)=\int_{(x-n)/h}^{(x-m)/h}u^ik(u)du\)。在编程序的时候，也只需把积分的上下限进行相应的调整即可。

四、参考文献

Jeffrey S. Simonoff, 1998. Smoothing Methods in Statistics. Springer-Verlag：http://pages.stern.nyu.edu/~jsimonof/SmoothMeth/