本文作者为中国人民大学统计学院饶燕芳同学,由COS编辑部审核发表,略有修改。点击此处下载/阅读本文PDF版本
一、问题的引出
在数据分析和数据建模的过程中,我们通常需要假定数据变量服从某种分布,以便于建立与分布参数有关的模型或方程,之后利用观测值对参数进行估计,从而达到研究和分析的目的。由于变量是随机的,我们无法确定变量在某个情况下的具体取值,因此通过假定它服从某个分布,然而感兴趣的只是它们的平均水平,即各变量之间的关系都建立在均值的基础上,方差则用于计算估计的精度和假设检验。而大多数情况下,一旦分布的假定确定,随之确定的也就是数据必须符合该分布的均值和方差特征。对于许多单参数分布,均值和方差均有一一对应的关系,如果均值确定,方差由于是均值的函数也就自然地确定下来,例如伯努利分布具有单参数\(p\),均值\(\mu=p\),方差\(v=p(1-p)\),即有\(v=v(\mu)=\mu(1-\mu)\)。在这种单参数的情况下,如果观测数据的均值符合假定(即认为\(p\approx\bar{Y}\)),数据的方差和均值就必须满足一定条件(即例如假定\(Y\)服从两点分布,认为\(p\approx\bar{Y}\),则方差应该有\(Var(Y)=p(1-p)\approx\bar{Y}(1-\bar{Y})\)),此时若观测到方差系统地大于分布假设下(此时常被观测均值决定)的方差,就出现了所谓的“超散布性”(overdispersion),类似地,若出现方差偏小的情况,也就相应出现了“超聚集性”(underdispersion)。
具体到本文需要讨论的泊松分布:现实中常常出现方差不满足假定的情况。由于参数为 的泊松分布具有均值和方差相等的特点,如果假定服从泊松分布的数据的样本方差大于模型估计的方差——即样本均值,就出现了“超散布性”,本文称之为泊松分布高方差(extra-Poisson variation),而当样本方差低于样本均值时,称此时的“超聚集性”为泊松分布低方差,后文出现的泊松低方差都符合该定义。
正如之前所说,通常建立模型如线性回归都基于均值,因此方差违反假定分布并不影响参数估计效率,但在区间估计和假设检验时就会出现问题。当“超聚集性”出现时,真实的方差会被低估,这将会错误的表现出数据中原本不显著的差异,相反地,“超聚集性”出现时,真实的方差会被高估,这样可能无法检验出组间分布的真实差异,参数的置信区间也会给得过大。因此对于方差超扩散或超聚集的数据,方差问题的处理显得尤为重要,针对此的模型建立是该类问题分析的关键。
泊松分布的超散布性数据在现实中较为常见,简单的序列正相关和非齐次性都可能引起超散布性的出现。泊松低方差的情况则较为少见,但在医学和社会领域中却经常出现。本文的目标就在于探讨针对泊松低方差数据的分布模型。
二 两种泊松低方差问题的处理方法
泊松分布为模拟计数数据提供了良好的模型,但均值和方差相等的要求在现实中却显得太为苛刻。因此处理泊松低方差的方法探究就集中在合适的修正分布的寻找上。能够描述计数数据且具有泊松低方差特点(即均值大于方差)的分布选择并不太多,其中包括两种典型的泊松低方差模型:加权泊松分布模型和 CBR 分布模型。
1. 加权泊松分布
Rao CR (1965)提出,若随机变量Y服从加权泊松分布,其密度函数为
$$P(Y=k)=\frac{e^{-\lambda}\lambda^k\omega_k }{Wk!}, k=0,1, \ldots ; \lambda>0$$
\begin{equation} W=\sum^{\infty}_{k=1}\frac{e^{-\lambda}\lambda^k\omega_k }{k!}\label{a} \end{equation}
它是保证求和为1的标准化因子。
本文讨论一种较为简单的权重(Martin S R and P Besbeas,2004),即
$$\omega_k=\left( \begin{array}{ll} e^{\beta_1(\lambda-k)} & ,k\leq\lambda\\e^{\beta_2(\lambda-k)} & ,k>\lambda\\\end{array} \right)$$
对于\(\beta_1,\beta_2>0\),它的分布类似将概率密度图线向均值“挤压”(见图1),分布更加集中,相对于标准的泊松分布就有更小的方差,称该分布为三参数指数加权泊松分布,记为 EWP3 。特殊地,当\(\beta_1=\beta_2=\beta\)时,称为两参数指数加权泊松分布,记为 EWP2 分布,当\(\beta=0\)时退化为标准泊松分布。对于EWP2 和 EWP3 ,它们拥有更高的峰值,标准化因子 W 可以由式 \ref{a} 导出。尽管矩的表达没有显式,但可以确定分布的方差随着\(\beta_1,\beta_2\)或\(\beta\)的增大而降低。
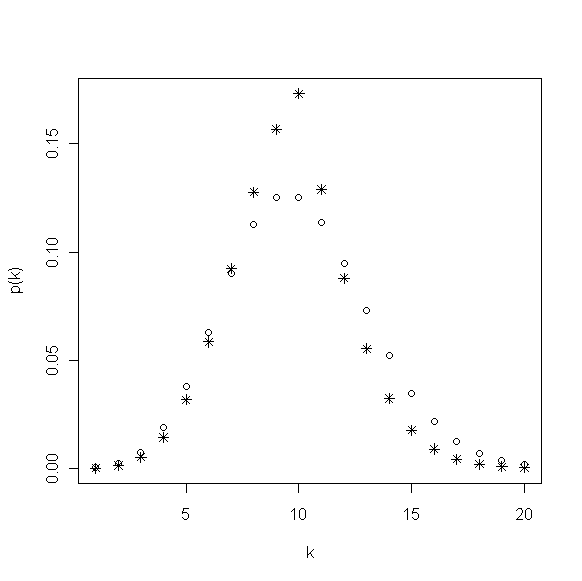
图1 lambda=10,beta1=0.1,beta2=0.2的EWP分布
对于加权泊松分布的探究使得权重还有一些别的形式,如 Castillo and Pe´rez-Casany (1998) 提出的幂加权泊松分布(PLWP),Cameron 和 Johansson (1997) 使用的泊松多元加权分布 PPp 等。
2. 纯生过程模型(CBR)
不得不提的是,在处理泊松低方差数据的问题中还有一类较为有效的方法。由Faddy(1997)在随机过程的基础上提出这种变出生概率(CBR)分布。这个分布是建立在广义泊松分布的基础上:Faddy 认为,任何关于 {0,1,2,…}的离散分布都有广义泊松特性,即纯生过程。考虑一个 Markov 计数过程,\(X(t)\)为\((0,t)\)内的事件发生数,在\((t,t+\sigma t)\)内有转移概率:
$$ P\left(X(t+\sigma)=n+1|X(t)=n\right)=\lambda_n\sigma+o(\sigma)$$
其中\(\lambda_n\)为事件数为n时的事件发生率,我们感兴趣的只是某一时刻\(X(t)\)的分布,这里t可以不失一般性地取1,在此模型中,时刻1时的事件数\(X\)的分布具有如下形式:
$$(p_1(1),p_2(1),\ldots,p_n(1))=(1,0,0,\cdots,0)exp(Q)$$
其中
$$p_i(1)=P\left(X(1)=i\right)$$
$$exp(Q)=e^Q=E+\frac{Q}{1}+\frac{Q^2}{2!}+\frac{Q^3}{3!}+\cdots$$
$$ Q=\left( \begin{array}{ccc} -\lambda_1 & \lambda_1 & 0 & \ldots & 0\\0 &-\lambda_2 & \lambda_2 & \ldots & 0\\0 & 0 & -\lambda_3 & \ldots & \vdots\\ \vdots & \vdots & \vdots & \ddots & \lambda_{n-1}\\ 0 & 0 & 0 & \ldots & -\lambda_n\\\end{array} \right)$$
而上式的成立可由 Kolmogorov 微分方程简单推导而来:
$$p'(t)=Qp(t); p(t)=ce^{Qt}; p(1)=ce^Q;$$
$$p(0)=c; p(1)=p_0e^Q; p(0)=(1,0,0,\ldots,0)$$
这里认为初始时刻的事件数是从1开始的。因此,CBR 分布是由一系列不同的事件发生率参数\(\left(\lambda_1,\lambda_2,\ldots,\lambda_k,\ldots\right)\)决定的。通常可以认为\(\lambda_k\)是k的函数。Faddy 在1997年已经证明,对于递增的\(\left(\lambda_1<\lambda_2<\cdots<\lambda_n<\cdots\right)\),\(X(t)\)将表现出泊松高方差特征,而当\(\lambda_1>\lambda_2>\cdots>\lambda_n>\cdots\)递减时,也就表现出泊松低方差特征。
三、参数估计
上述两种分布的参数估计都可通过极大似然法求出。记\(x_i\)为第i个样本的事件发生数,观测数据中中事件数k的频数\(f_k\)(k=1,2,3,…),则 EWP2 和 EWP3 分布的负对数似然方程为(已去除与参数无关的项\(lnk!\)):
\begin{equation} -LnL(\lambda,\beta_1,\beta_2)=n[\lambda-\bar{x}ln\lambda+lnW]+\beta_1\sum^{[\lambda]}_{k=x_{min}}(\lambda-k)f_k+<br /> \beta_2\sum^{x_{max}}_{k=[\lambda]+1}(k-\lambda)f_k \label{b} \end{equation}
通过求使 \ref{b} 式达到最小值的\(\hat{\lambda},\hat{\beta}_1,\hat{\beta}_2\)得到估计参数。
对于纯生过程模型,概率分布向量\((p_1(1),p_2(1),\ldots,p_N(1))\)就是矩阵\(exp(Q)\)的第一行,若\(N=x_{max}\),其负对数似然函数为:
$$-LnL(\lambda_1,\lambda_2,\ldots,\lambda_N)=\sum^N_{k=1}f_klnp_k(1)$$
通过最小化上式即可得到\((\lambda_1,\lambda_2,\ldots,\lambda_N)\)的极大似然估计。而参数估计的方差可以通过数值计算时产生的 Hessian 矩阵得到。
四、数据实例
我们引用 Faddy(2001)的小鼠胚胎数据,作者已对该数据用 CBR 方法做了较好的分析。在产生该数据的实验中,对已经怀孕的小鼠用药(除草剂2,4,5-T),同时记录小鼠子宫上的胚胎着床数。数据给出了7种剂量水平下胚胎着床数的频率分布。在交配后的6-14天内,往怀孕的雌鼠体内注射某种剂量水平的2,4,5-T。在分娩之前,将雌鼠杀死,确定其体内的活胎数目。0剂量组的频数分布便具有泊松低方差特征。0剂量组数据的均值为11.55,方差为9.92,方差均值比为0.859。
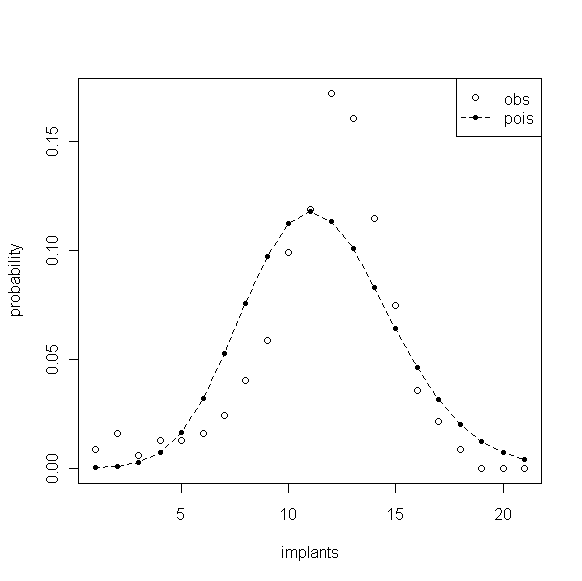
图2
使用泊松分布对参数进行估计,参数 的最大似然估计为样本均值11.55,图2显示了估计的泊松分布和样本观测频率的差异。尽管拥有相同的均值,但由于数据具有泊松低方差特点,其经验分布的比泊松分布集中得多,可以说此时使用泊松分布模型的效果是差强人意的,显然不是一个合适的模型。
1. 加权泊松分布
分别使用 EWP2 和 EWP3 分布对0剂量组数据进行参数的最大似然估计。其中EWP2分布中,\(\hat{\lambda}= 11.79\), \(\hat{\beta}=0.11\),EWP3中,\(\hat{\lambda}=14.56\),\(\hat{\beta}_1=-0.15\),\(\hat{\beta}_2=0.68\),估计的 EWP2 、EWP3 分布如图3。由于分布具有了泊松低方差特征,通过权重参数\(\beta(\beta_1,\beta_2)\)将分布向中部“挤压”,分布更加集中且峰值更高,估计的效果相比之下比泊松分布好很多。EWP2 由于在 \(\lambda\) 的左右都赋予相等的权重,因此对称的“压缩”模式不如 EWP3 的非对称“压缩”有弹性,从观测数据经验分布的轻微左偏也暗示了允许\(\beta_1,\beta_2\)取不同值的 EWP3 分布在分布的拟合上更具优势。
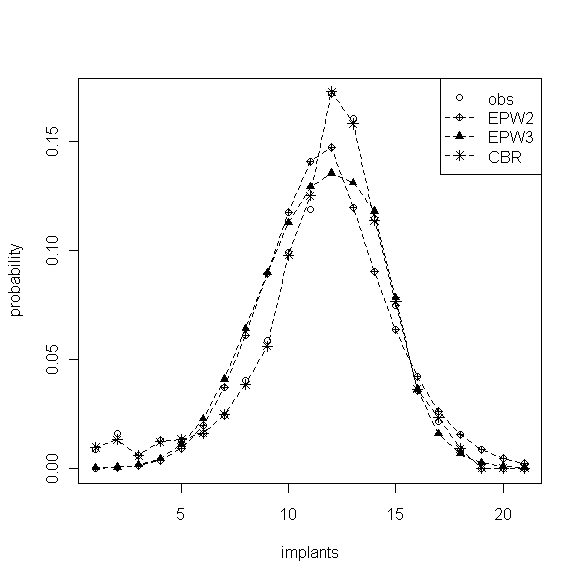
图3 EWP2 、EWP3和CBR的分布拟合图
2. CBR分布
CBR参数的极大似然估计\(\hat{\lambda}_1,\hat{\lambda}_2,\ldots,\hat{\lambda}_{21}\)= {4.66, 7.90, 22.97, 15.02, 18.23, 19.18, 16.49, 14.40, 13.15, 10.01, 9.33, 6.90, 6.32, 6.26, 5.40, 6.28, 3.27, 0.00, 2.00, 2.00, 1.00},图3中显示的 CBR 拟合效果非常好,几乎与经验分布重合。但模型中含有过多的参数使得估计精度大大降低,其中\(\hat{\lambda}_3\)的估计标准误为12.59,置信区间宽近50。虽然对于拥有多个事件发生率\(\hat{\lambda}_k\)的 CBR 分布能够灵活地刻画事件发生数之间的任何概率变化,但参数时过多模型的过度拟合是没有太大意义的,也不易于控制和分析。如前所述,可以利用该模型的\(\lambda\)建立关于k的函数,从而减少模型中的参数个数,在该例子中事件数分类较多时这种做法就显得十分必要。Faddy(2001) 就从众多函数形式中找到了一种能很好地模拟事件数发生概率在最初增长较快而后缓慢下降特点的四参数模型:
$$\lambda_k=a(k^be^{-ck}+d), k\geq1$$
对于0剂量组数据,\(\left(a,b,c,d\right)\)的估计值为 {1.360, 3.507, 0.648, 2.953},估计的分布与经验分布的对比如图4,尽管模型中减少了17个参数,但由于函数形式的合理,该分布仍旧保持较好的拟合效果,拟合优度\(\chi^2(13)=6.755\),p值为0.914。
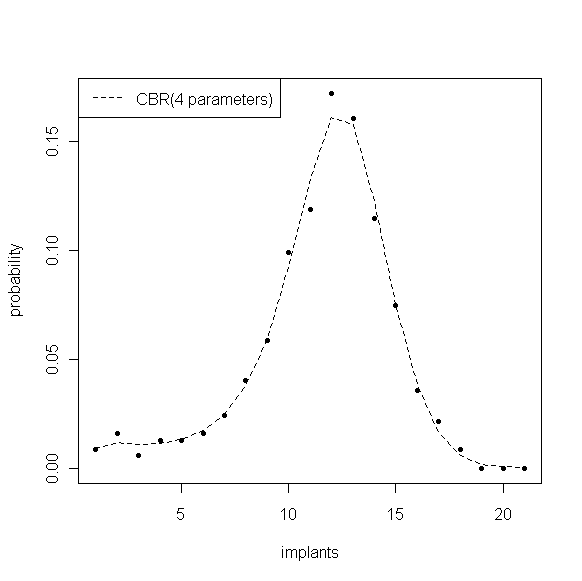
图4
针对 2-4-5T 对小鼠胚胎着床影响的实验数据的泊松低方差特性,相对于标准泊松,加权泊松 EWP2、EWP3 和 CBR 在分布上的修正都使模型有许多改进,能够更好地表现出数据中蕴含的现实含义,其生物学意义的解释也更加清晰:在发育毒性的研究中,药物会影响早期的繁殖过程,阻止胚胎的形成。对于多胎的动物(如老鼠),参数起初的增长表示了受精胚胎着床过程可以进一步刺激排卵,之后的下降说明受精卵着床过程的减慢,这段平缓的过程也就使得方差有所降低。
3. 组别分析
之所以选择一个足够合适的分布的重要的意义不仅在于它能较合适地刻画观测数据,更在于它能够精确地刻画不同组别之间的差异。Faddy(2001)表明75剂量组和90剂量组的频数分布相似,并不存在显著性的差异,文章这部分就将比较标准泊松、EWP2、EWP3 和 CBR 这四种分布在检验0剂量组和75/90剂量组之间差异的能力。过程中使用似然比检验。
似然比检验在大样本时具有渐进性。似然比统计量为
$$\Lambda(x)=\frac{sup{L(\theta|x):\theta\in\Theta_o}}{sup{L(\theta|x):\theta\in\Theta}}$$
当样本量n趋于无穷,\(-2log(\Lambda)\)将渐进服从\(\chi^2(r)\)分布,r为参数空间\(\Theta\) and \(\Theta_o\)的维数之差。
表1 四种分布检验效果比较
\(-2log(\Lambda)\) |
自由度r | p值 | |
|---|---|---|---|
| 标准泊松 | 2.690 | 1 | 0.1000 |
| EWP2 | 4.789 | 2 | 0.0912 |
| EWP3 | 11.980 | 3 | 0.0075 |
| CBR | 10.764 | 4 | 0.0294 |
标准泊松分布的0剂量组和75/90剂量组的极大对数似然函数值分别为-1837.763和-318.618 ,即负两倍似然比为2.691(自由度为1),p值为0.10(实际值大于0.1),即使在10%的显著性水平上都无法认为0剂量和75/90剂量对小鼠胚胎着床的影响是显著的。EWP2 的负两倍似然比为4.789,p值比标准泊松略小,为0.0912,在10%的显著性水平下可以认为0剂量组和75/90剂量组小鼠胚胎着床的显著差异,但如果显著性水平在5%则无法拒绝原假设。相比之下,CBR和EWP3的负两倍似然比统计量的p值都小得多,在通常5%的显著性水平下能够有力地表明0剂量组和75/90剂量组之间的差异是显著的,且其中 EWP3 的检验效率甚至明显高于 CBR,p值0.0075达到高度显著。
以上检验至少说明在0剂量组和75/90剂量组的比较上 EWP2、EWP3 和 CBR 都优于标准泊松,能够有效地检测出不同组别之间的分布差异,从而证明了本文之初的观点:标准泊松无法准确刻画该实验数据具有泊松低方差的特性,因此将高估剂量组内的方差,在检验上无法有效地识别组间真实存在的差异。如果轻易地使用泊松分布进行分析,将得出0剂量组和75/90剂量组无显著差异的错误结论。而加权泊松分布和 CBR 都在某种程度上克服了标准泊松的缺点,其中 EWP3 和 CBR 则“灵敏”地发现了组间的显著性不同。且 EWP3 能够表现地比 EWP3 出色,还因为剂量组下的频数分布略微左偏,2个加权参数容许 EWP3 更贴切地拟合原始数据的真实分布。
五、结论
当数据出现“超散布性”和“超聚集性”时可能出现的问题,分布假定的错误将分别低估和高估真实数据的方差,从而影响模型的合理性,有时甚至导致得出错误的结论。本文着眼于一类典型的“超聚集性”问题——泊松低方差特性,并针对该类问题的解决归纳了两种方法:泊松加权分布模型和纯生过程分布模型。前者通过对标准泊松分布进行加权修正,克服了泊松分布均值和方差必须相等的局限性,其中 EWP2 和 EWP3 具有形式简单且适用性强的特点,而 EWP3 在很多情况下会优于 EWP2,多一个参数能够较好地模拟较普遍的不对称的单峰经验分布。而纯生过程分布模型在思路上则有很大不同,它基于随机过程中的事件发生机制,对于分类的事件计数数据在理论上有很强的适用性。CBR 能够用足够多的参数\(\lambda_k\)模拟不同事件数间频率的变化特征,通过建立\(\lambda_k\)与k的合适的函数形式,可以构造出任何离散分布,尤其适和分析分类较多的数据。此外,\(\lambda_k\)的函数变化还有利于结合数据在真实世界中的内在的形成原理,对基于不同事件数时刻的时间发生率\(\lambda_k\)有比较完整的描述,能够赋予参数合理的解释。但 CBR 不适用于分类较少的计数数据,会由于缺少事件产生过程信息它无法表现出其优势。

发表/查看评论