$$ \def\ind{{\perp\!\!\!\perp}} \def\nind{{\not\!\perp\!\!\!\perp}} $$
这一节介绍一个有趣的历史性例子:吸烟是否导致肺癌?主要涉及的人物是 R A Fisher 和 J Cornfield。前者估计上这个网站的人都听过,后者就显得比较陌生了。事实上,Cornfield 在统计、生物统计和流行病学都有着非常重要的贡献。来自 Wikipedia 的一句介绍:“He was the R. A. Fisher Lecturer in 1973 and President of the American Statistical Association in 1974.” 虽然 Cornfield 和 Fisher 学术观点不同(本节介绍),但是 Cornfield 还是在 1973 年给了 Fisher Lecture。
下面我们先介绍 Fisher 和 Cornfield 关于观察性研究中因果推断的两种观点,再给出技术性的细节。
一、Cornfield 条件或者 Cornfield 不等式

(图注:R A Fisher)
我先陈述 Fisher 的观点。由于 Yule-Simpson Paradox 的存在,即使我们观测到吸烟和肺癌之间的正相关关系,也不能断定它们之间有因果性。可能存在一个未观测的基因,它既使得某些人更可能吸烟,又使得这些人更可能患肺癌。因此,即使吸烟和肺癌没有因果关系,这个未观测的基因也可能导致吸烟和肺癌是正相关的。关于 Yule-Simpson Paradox,这一系列的第一篇有介绍。Fisher 的观点可以用一个有向无环图 (DAG) 来表示:
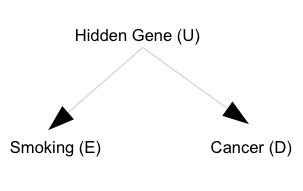
图中,吸烟到肺癌没有直接的边,因此吸烟对肺癌的因果作用是 \(0\)。但是由于它们之间存在一个共同原因 “hidden gene”,它们是相关的。我们用 \(E\) 表示是否吸烟 (\(1=\) 是,\(0=\) 否);\(D\) 表示是否患肺癌 (\(1=\) 是,\(0=\) 否);\(U\) 表示是否有某种基因 (\(1=\) 是,\(0=\) 否)。这个符号系统在流行病学比较常用,因为 \(E\) 表示暴露与否 (exposure),\(D\) 表示疾病 (disease),\(U\) 表示未观测的混杂因素 (unobservable confounder)。 在 Fisher 的时代,研究者通过收集的大量数据,得到吸烟对于肺癌的相对风险(relative risk;或称风险比,risk ratio;都简写成 \(RR\))是
$$ RR_{ED}= \frac{ P(D=1\mid E=1) } { P(D=1\mid E=0) } = 9. $$
流行病学家关心这个 \(RR_{ED}\) 是否表明了吸烟和肺癌的因果关系。Fisher 表示否定。从一个悲观的角度来讲,我们确实不能从相关关系得到因果性;Fisher 如果表示怀疑,假定有一个未观测的基因,也是无可反驳的。Fisher 的这个说法有时也被称为“共同原因”假说。Cornfield 则采取了一个不太悲观的角度。他问:如果 Fisher 的“共同原因”假说是对的,那么 \(E\) 和 \(U\) 之间的相关关系需要多强,才能导致 \(RR_{ED} = 9\),即“吸烟患肺癌”是“不吸烟患肺癌”的风险的 \(9\) 倍呢?如果 \(E\) 和 \(U\) 之间的相关关系强到不具有生物学意义(\(E\) 与 \(U\) 的相对风险值大得在现实中不太可能),那么 Fisher 的“共同原因”假说就不成立,更大的可能性是吸烟 \(E\) 对肺癌 \(D\) 有因果作用。
那么 Cornfield 是如何有力反驳Fisher的观点的呢?

(图注:J Cornfield)
Cornfield 通过简单的数学证明,得到了如下的不等式,文献中也称为 Cornfield 不等式:
$$ RR_{EU} \geq RR_{ED}. $$
也就是说,如果 Fisher 的“共同原因”假说成立,那么 \(E\) 和 \(U\) 之间的 \(RR\) 必将大于 \(E\) 和 \(D\) 之间的 \(RR\)。在吸烟和肺癌的例子中,\(RR_{EU} \geq 9\)。\(RR_{EU} \geq 9\),即 \(P(U=1|E=1)/P(U=1|E=0) \geq 9\),直观解释就是“吸烟时有某个基因 \(U\) 存在”的概率是“不吸烟时有某个基因 \(U\) 存在”的概率的 \(9\) 倍多。根据 Cornfield 进一步的逻辑,由于吸烟更多的是一个社会性的行为,很难想象吸烟的行为能够对于某个基因的存在与否有着 \(9\) 倍的预测能力。我前段时间问身边一个生物的 PhD,你觉得 \(RR_{EU} \geq 9\) 可能吗?他的回答是不太可能,理由也是说,吸烟更多的决定于社会经济地位、家庭背景等变量,和基因也许有关系,但是不会强到 \(RR_{EU} \geq 9\) 的程度。Cornfield et al. (1959) 的原话是:
… if cigarette smokers have 9 times the risk of nonsmokers for developing lung cancer, and this is not because cigarette smoke is a causal agent, but only because cigarette smokers produce hormone X, then the proportion of hormone-X producers among cigarette smokers must be at least 9 times greater than nonsmokers. If the relative prevalence of hormone-X-producers is considerably less than ninefold, then hormone-X cannot account for the magnitude of the apparent effect.
如果我们相信 Cornfield 的逻辑,\(RR_{EU} \geq 9\) 在生物学意义上不太可能,那么 Fisher 的“共同原因”假说就不成立,吸烟对肺癌的确存在因果作用;反映到上面的 \(DAG\) 上,吸烟 \(E\) 到肺癌 \(D\) 有一条直接的边。
Cornfield 的这项简单研究,开始了流行病学和统计学中敏感性分析的研究;比如 Rubin 和 Rosenbaum 很多工作都是在 Cornfield 的启发下做出来的。简单地说,敏感性分析,就是在朝着 Yule-Simpson Paradox 的反方向进行的:复杂虽然总是存在,但是我们相信这个世界并不是疯狂的复杂。
二、技术细节
这一部分我们给出 Cornfield 不等式的证明。虽然证明不难,但是想想 Cornfield 于 1959 年用这样一个简单的不等式来反驳 Fisher,就觉得它的历史意义还是不小的。当然不关心技术细节的读者,可以直接忽略本节。关心技术细节的读者,下面的证明虽然冗长,但是只用到非常初等的数学(也许它可以作为一道初等概率论的习题)。
为了简化证明,我们引进一些记号:
$$ \begin{eqnarray} f_1 = P(U=1\mid E=1), &&f_0 = P(U=1\mid E=0),\\ RR_{EU} = \frac{ P(U=1\mid E=1) }{ P(U=1\mid E=0)} = \frac{f_1} {f_0}, && RR_{UD} = \frac{ P(D=1\mid U=1) }{ P(D=1\mid U=0) }. \end{eqnarray} $$
不妨假设 \(RR_{ED}\geq 1\) 并且 \(RR_{EU} \geq 1\);若不成立,我们总可以重新对这些二值变量的 \(0\) 和 \(1\) 类进行重新定义。首先,我们在条件独立性 \(E\ind D|U\) 下得到 \(RR_{ED}\) 的等价表示:
$$ \begin{eqnarray} RR_{ED} &=& \frac{ P(D=1\mid E=1) } { P(D=1\mid E=0) }\\ &=& \frac{ \sum_{u=0,1}P(D=1, U=u\mid E=1) } {\sum_{u=0,1} P(D=1, U=u\mid E=0) }\\ &=& \frac{ \sum_{u=0,1}P(D=1\mid U=u) P(U=u\mid E=1) } {\sum_{u=0,1} P(D=1\mid U=u) P(U=u\mid E=0) }\\ &=& \frac{ P(D=1\mid U=1)P(U=1\mid E=1) + P(D=1\mid U=0)P(U=0\mid E=1) } { P(D=1\mid U=1)P(U=1\mid E=0) + P(D=1\mid U=0)P(U=0\mid E=0) }\\ &=& \frac{ RR_{UD} f_1 + (1-f_1)}{ RR_{UD} f_0 + (1-f_0)}. \end{eqnarray} $$
条件 \(RR_{EU}\geq 1\) 等价于 \(f_1\geq f_0\),因此,上面 \(RR_{ED}\) 是关于 \(RR_{UD}\) 的单调递增函数。进一步,
$$ RR_{ED} \leq \lim_{RR_{UD}\rightarrow +\infty} \frac{ RR_{UD} f_1 + (1-f_1)} { RR_{UD} f_0 + (1-f_0) } = \frac{f_1}{f_0} = RR_{EU}. $$
由此,Cornfield 不等式得证。
三、文献注记
Cornfield 最早的论文发表于 1959 年;由于它的重要性,这篇文章又在 2009 年重印了一次(50 周年纪念)。于是参考文献有两篇,它们是一样的;不过后者多了很多名人的讨论。
- Cornfield J et al. Smoking and lung cancer: recent evidence and a discussion of some questions. JNCI 1959;22:173-203.
- Cornfield J et al. Smoking and lung cancer: recent evidence and a discussion of some questions. Int J Epidemiol 2009;38:1175-91.(本文邀请了 David R Cox 和 Joel B Greenhouse 等人讨论。)
最近 Ding and VanderWeele 重新回访了这个经典问题,给出了更加广泛的结果。
- Ding, Peng and Vanderweele, Tyler J. (2014). Generalized Cornfield conditions for the risk difference, Biometrika, 101:4, 971-977. https://doi.org/10.1093/biomet/asu030


发表/查看评论