$$ \def\ind{{\perp\!\!\!\perp}} \def\nind{{\not\!\perp\!\!\!\perp}} $$
在充满随机性的统计世界中,悖论无处不在。这一节介绍一个很有名,但是在中文统计教科书中几乎从未介绍过的悖论。这个悖论是 Educational Testing Service (ETS) 的统计学家 Frederic Lord 于 1967 年提出来的;最终由同在 ETS 工作的另外两位统计学家 Paul Holland 和 Donald Rubin 于 1982 年圆满地找出了这个悖论的根源。这部分先介绍这个悖论,再介绍 Holland 和 Rubin 的解释,最后是一些结论。
一 Lord’s Paradox
考虑下面一个简单例子,具体的数字是伪造的。某个学校想研究食堂对于学生体重是否有差异性的影响,尤其关心食堂对于男女学生体重影响是否相同。于是统计学家们收集了如下的数据:学生的性别$G$;学生在 1963 年 6 月入学时候的体重$X$;学生在1964年6月放暑假时候的体重$Y$。
第一个统计学家,采取了一种很简单的方法。如图所示,横轴表示1963年6月入学前的体重$X$,纵轴表示1964年6月前放假的体重$Y$。个体上来看,男女入学前和入学后一年体重都会有些变化,男女学生体重的散点图分别用绿色和红色标出。从男女学生生平均体重来看,男生入学前后一年平均体重均是150磅(图中右上角的黑点),女生入学前后一年平均体重均为130磅(图中左下角的黑点)。图中的虚线是对角线$Y=X$,两个黑点均位于对角线上。因此,第一个统计学家的结论是食堂对于男女学生体重都没有影响,因此对男女学生体重的作用相同。
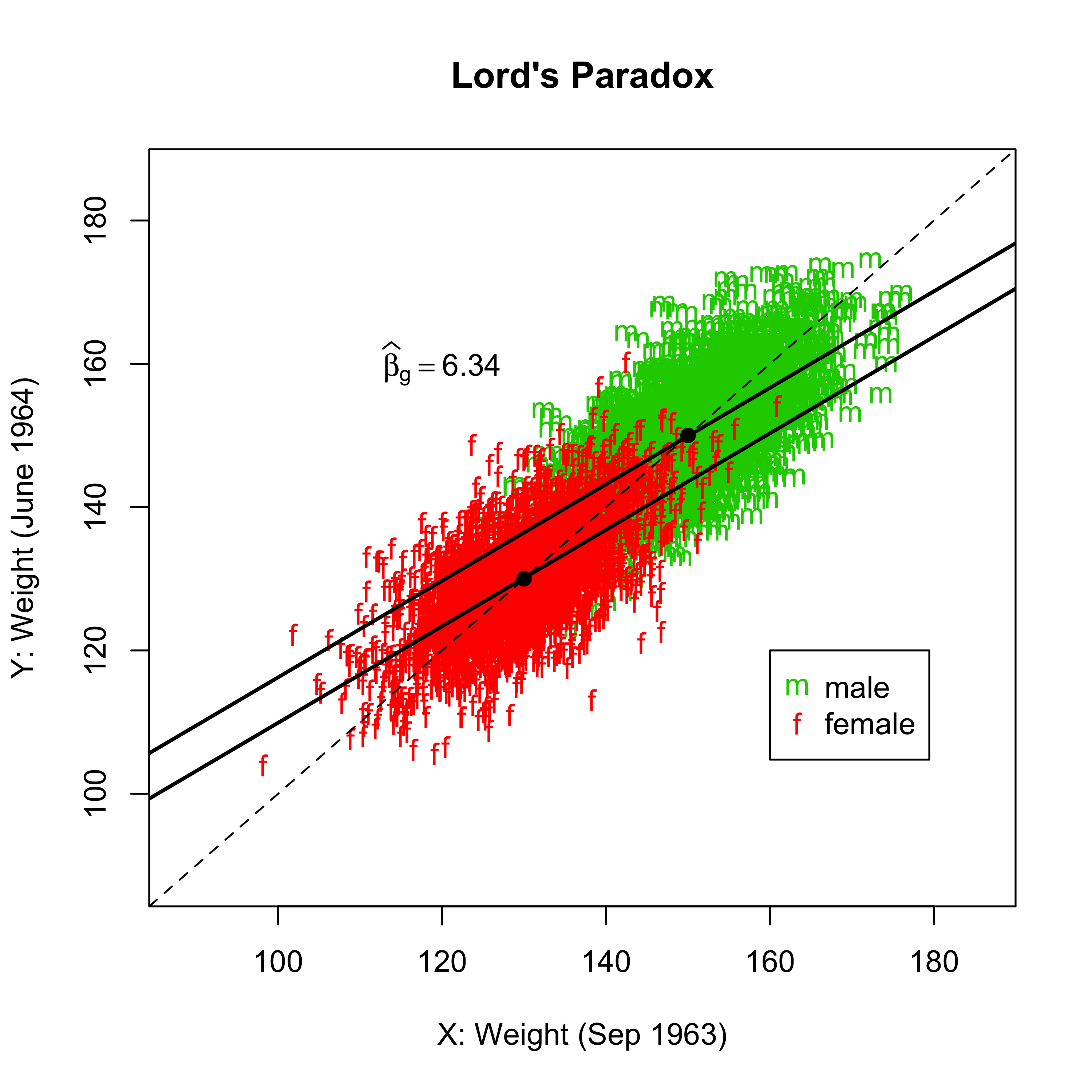
(图注:横轴表示1963年6月入学前的体重$X$,纵轴表示1964年6月前放假的体重$Y$;虚线是对角线$Y=X$;男女学生体重的散点图分别用绿色和红色标出。图中数据生成机制如下:男学生$(X,Y)\sim$二元正态分布,均值$(150,150)$,协方差矩阵$\begin{pmatrix} 60 & 40 \\ 40 & 60 \end{pmatrix}$;女学生$(X,Y)\sim$二元正态分布,均值$(130,130)$,协方差矩阵$\begin{pmatrix} 60 & 40 \\ 40 & 60 \end{pmatrix}$。生成这幅图的 R 代码可以在这里下载:Rcode。由于样本量3000,样本均值非常接近理论均值,因此落在了对角线上。)
第二个统计学家,由于受到了高等的统计训练,知道 R A Fisher 的 Analysis of Covariance (ANCOVA) ,提出了更加复杂的方法。他认为,我们的分析应该控制入学前的体重,做如下的线性回归:
$$ Y_i = \beta_0 + \beta_g G_i + \beta_x X_i + \varepsilon_i. \quad\quad\quad (*) $$
他进一步认为,上面线性回归的系数$\beta_g$反应的就是男女的差别。用最小二乘法拟合上面的回归模型,等价于在男女学生中拟合两条平行的回归直线。如图所示,两条直线斜率$\beta_x$相同,但是截距不同,截距之差就是回归系数$\widehat{\beta}_g = 6.34$。结论是,食堂对于男女体重有差别性的影响。
这两位统计学家得到了不同的结论,究竟谁对谁错呢?Lord 称这个现象为悖论,那么悖论的根源是什么呢?
二 悖论的根源:因果推断视角下的解释
要想解释这个悖论,使用线性回归模型益处不大,因为究竟能否将回归系数解释成因果作用,是个根本性的问题。在下面的讨论中,我们假定数据的样本量足够大,因而可以忽略小样本带来的随机性;也可以认为整个讨论都在总体上进行。和前面一样,我们用$G_i$表示个体$i$的性别,男性取值为1, 女性取值为0;$X_i$是个体 $i$在 1963 年 9 月的体重。由于这两个变量都发生在接受处理(在食堂进餐与否)之前,它们都可以看成是协变量,不受处理的影响。我们采用潜在结果模型,定义 $\{ Y_i(1), Y_i(0) \} $是个体 $i$ 在食堂进餐和不在食堂进餐下于 1964 年六月体重的潜在结果。
如果用$T$表示在食堂进餐与否的变量,那么每个学生都是$T=1$。当写下潜在结果之后,我们就发现问题的根源之一,是整个研究根本不存在对照组(全体学生其实都在食堂进餐),每个个体在 1964 年 6 月都取值$Y(1)$(也就是前面的记号$Y$)。
继续我们的讨论。男女学生的平均因果作用分别定义为:
$$ \Delta_g = E\{ Y(1) – Y(0) \mid G = g \}, g=1, 0; $$
食堂对于男女学生体重平均因果作用的差是:
$$ \begin{eqnarray} \Delta &=& \Delta_1 – \Delta_0\\ &=& E\{ Y(1) – Y(0) \mid G = 1 \} – E\{ Y(1) – Y(0) \mid G = 0 \}\\ &=& \left[ E\{ Y(1) \mid G = 1 \} – E\{ Y(1) \mid G = 0 \} \right] \\ && – \left[ E\{ Y(0) \mid G = 1 \} – E\{ Y(0) \mid G = 0 \} \right]. \end{eqnarray} $$
上面的推导虽然简单,但是将$\Delta$分成了两个显著不同的部分:第一个方括号内的项是我们能够从观测数据中得到的;第二个方括号中的项是我们不可观测的,因为没有任何一个学生接受了食堂之外的处理。
如果我们假定$Y(0) = X$,也就是说如果学生不来食堂进餐,他们的体重将和入学前一样,那么
$$ \Delta_g = E\{ Y(1) – X\mid G = g \} = E(Y-X\mid G=g). $$
根据上面的图和统计学家一的推理逻辑,我们知道$\Delta_g = 0 (g=0,1)$(男女学生的体重不受处理影响),那么$\Delta = 0$(处理对于男女体重没有差异性的影响)。在这个假定下,第一个统计学家的断言是正确的。
显然,假定$Y(0) = X$是无法被数据证明或者证伪的,它只能依赖于我们的先验知识。那么在什么假定下,第二个统计学家又是对的呢?
根据第二个统计学家做 ANCOVA 的逻辑,他可以假定
$$ E\{ Y(1)\mid X, G= g \} = a_g + bX, $$
并且把$\delta = a_1 – a_0$当成食堂对于男女体重差异作用的度量。$\delta$其实就是上面的线性回归模型$(*)$的回归系数$\beta_g$。如果我们假定 $Y(0) = \alpha + b X$,那么不去食堂进餐时的潜在体重$Y(0)$是入学前体重$X$的线性函数且截距是$b$;这表明$Y(1)$和$Y(0)$关于$X$的模型,仅仅截距不同,斜率相同。这个假定并非不可能。此时,
$$ \begin{eqnarray} \Delta &=& E\{ Y(1) – Y(0) \mid G=1\} – E\{ Y(1) – Y(0)\mid G=0\} \\ &=& E\{ Y(1) – \alpha – bX \mid G=1\} – E\{ Y(1) – \alpha – bX\mid G=0\} \\ &=& \left[ E\{ Y(1) \mid G=1\} – b E(X\mid G=1) \right] \\ &&- \left[ E\{ Y(1)\mid G=0\} – b E(X\mid G=0) \right]\\ &=& a_1 – a_0 = \delta. \end{eqnarray} $$
最后一行等于$\delta$,因为根据条件期望的性质,方括号中的两项分别是$a_1$和$a_0$:
$$ \begin{eqnarray} && E\{ Y(1) \mid G=g\} – b E(X\mid G=g) \\ &=& E\left[ E\{ Y(1) \mid X, G=g\} \mid G=g\right] – b E(X\mid G=g) \\ &=& E\left[ a_g + bX \mid G=g\right] – b E(X\mid G=g) \\ &=& a_g. \end{eqnarray} $$
这样一来,第二个统计学家的结论就是正确的。
三 结论
根据上面的讨论,关于 Lord’s Paradox,我们有如下的结论:
(1)Lord’s Paradox 的根源在于,整个研究没有对照组;我们甚至不知道什么是对照组,不在食堂进餐,是在家里进餐,还是外面的参观进餐,还是其他?这其实导致 $Y(0)$ 并非完好定义。上面的讨论则是假定$Y(0)$是良好定义的。
(2)回归或者协方差分析等统计工具,并不能清楚的回答因果的问题。这个问题中,$\Delta$是一个我们关心的因果度量,离开潜在结果,是很难定义的。根据上面的讨论,两位统计学家不采用潜在结果模型,甚至没有意识到,这个研究根本的问题在于缺少对照。当然,如果我们能够做一个随机化的实验,有处理和对照组,那么回归分析也可能得到合理的答案。
(3)统计学家一和二,都可以是对的。他们结论的正确性,依赖于不同的假定;而这些假定本身是不可能被检验的。
(4)假定$Y(0)=X$可以减弱到$Y(0)=X+u, E(u)=0, u\ind G$;假定$Y(0)= \alpha + b X$可以减弱到$Y(0) = \alpha + bX + v, E(v) = 0, v\ind G$。当然,这都是细枝末节的问题。
(5)统计学家一和二,都是错的。他们有结论,但是却从未清楚地陈述结论回答的是什么问题。
(6)R A Fisher 在实验设计中提出了 ANCOVA,但是这个方法不是万能的。事实上,这个方法导致的问题,比它带来的功用更严重;这点以后再说。
四 参考文献
(1)Lord FM. A paradox in the interpretation of group comparisons. Psychol Bull. 1967;68:304–5. doi: 10.1037/h0025105.
(2)Holland, P.W., Rubin, D.B. (1983). On Lord’s paradox. In: Wainer, H., Messick, S. (Eds.), Principals of Modern Psychological Measurement. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 3–25.


发表/查看评论