
原文链接请点击这里
前面我们介绍了线性情况下的支持向量机,它通过寻找一个线性的超平面来达到对数据进行分类的目的。不过,由于是线性方法,所以对非线性的数据就没有办法处理了。例如图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
对于这个数据集,我可以悄悄透露一下:我生成它的时候就是用两个半径不同的圆圈加上了少量的噪音得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用\(X_1\)和\(X_2\)来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
$$a_1X_1 + a_2X_1^2 + a_3X_2 + a_4 X_2^2 + a_5X_1X_2 + a_6 = 0$$
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为\(Z_1 = X_1\),\(Z_2=X_1^2\),\(Z_3=X_2\),\(Z_4=X_2^2\), \(Z_5 = X_1X_2\),那么显然,上面的方程在新的坐标系下可以写作:
$$\sum_{i=1}^5a_iZ_i + a_6 = 0$$
关于新的坐标\(Z\) ,这正是一个 hyper plane 的方程!也就是说,如果我们做一个映射\(\phi:\mathbb{R}^2\rightarrow\mathbb{R}^5\),将\(X\)按照上面的规则映射为\(Z\),那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
再进一步描述 Kernel 的细节之前,不妨再来看看这个例子映射过后的直观例子。当然,我没有办法把 5 维空间画出来,不过由于我这里生成数据的时候就是用了特殊的情形,具体来说,我这里的超平面实际的方程是这个样子(圆心在\(X_2\)轴上的一个正圆):
$$a_1X_1^2 + a_2(X_2-c)^2 + a_3 = 0$$
因此我只需要把它映射到\(Z_1 = X_1^2\), \(Z_2=X_2^2\), \(Z_3=X_2\)这样一个三维空间中即可,下图(这是一个 gif 动画)即是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:
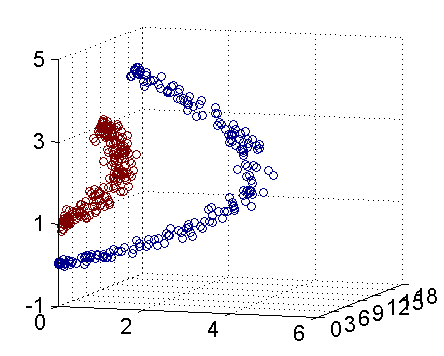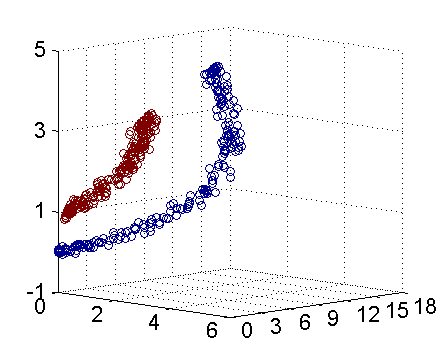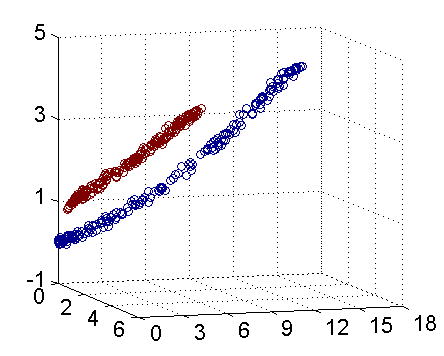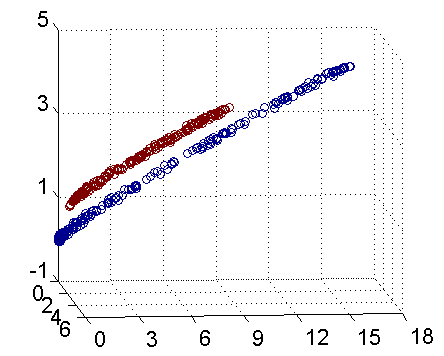
现在让我们再回到 SVM 的情形,假设原始的数据时非线性的,我们通过一个映射\(\phi(\cdot)\)将其映射到一个高维空间中,数据变得线性可分了,这个时候,我们就可以使用原来的推导来进行计算,只是所有的推导现在是在新的空间,而不是原始空间中进行。当然,推导过程也并不是可以简单地直接类比的,例如,原本我们要求超平面的法向量\(w\),但是如果映射之后得到的新空间的维度是无穷维的(确实会出现这样的情况,比如后面会提到的 Gaussian Kernel ),要表示一个无穷维的向量描述起来就比较麻烦。于是我们不妨先忽略过这些细节,直接从最终的结论来分析,回忆一下,我们上一次得到的最终的分类函数是这样的:
$$f(x) = \sum_{i=1}^n\alpha_i y_i \langle x_i, x\rangle + b$$
现在则是在映射过后的空间,即:
$$f(x) = \sum_{i=1}^n\alpha_i y_i \langle \phi(x_i), \phi(x)\rangle + b$$
而其中的\(\alpha\)也是通过求解如下 dual 问题而得到的:
$$ \begin{align} \[ \max_\alpha \] &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle \phi(x_i),\phi(x_j)\rangle \\ s.t., &\alpha_i \geq 0, i=1,\ldots,n \\ &\sum_{i=1}^n\alpha_iy_i = 0 \end{align} $$
这样一来问题就解决了吗?似乎是的:拿到非线性数据,就找一个映射\(\phi(\cdot)\),然后一股脑把原来的数据映射到新空间中,再做线性 SVM 即可。不过若真是这么简单,我这篇文章的标题也就白写了——说了这么多,其实还没到正题呐!其实刚才的方法稍想一下就会发现有问题:在最初的例子里,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维,那么我们会得到 19 维的新空间(验算一下?),这个数目是呈爆炸性增长的,这给\(\phi(\cdot)\)的计算带来了非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。所以就需要 Kernel 出马了。
不妨还是从最开始的简单例子出发,设两个向量\(x_1 = (\eta_1,\eta_2)^T\)和x_2=(\xi_1,\xi_2)^T,而\(\phi(\cdot)\)即是到前面说的五维空间的映射,因此映射过后的内积为:
$$\langle \phi(x_1),\phi(x_2)\rangle = \eta_1\xi_1 + \eta_1^2\xi_1^2 + \eta_2\xi_2 + \eta_2^2\xi_2^2+\eta_1\eta_2\xi_1\xi_2$$
另外,我们又注意到:
$$\left(\langle x_1, x_2\rangle + 1\right)^2 = 2\eta_1\xi_1 + \eta_1^2\xi_1^2 + 2\eta_2\xi_2 + \eta_2^2\xi_2^2 + 2\eta_1\eta_2\xi_1\xi_2 + 1$$
二者有很多相似的地方,实际上,我们只要把某几个维度线性缩放一下,然后再加上一个常数维度,具体来说,上面这个式子的计算结果实际上和映射
$$\varphi(X_1,X_2)=(\sqrt{2}X_1,X_1^2,\sqrt{2}X_2,X_2^2,\sqrt{2}X_1X_2,1)^T$$
之后的内积\(\langle \varphi(x_1)\),\(\varphi(x_2)\rangle\)的结果是相等的(自己验算一下)。区别在于什么地方呢?一个是映射到高维空间中,然后再根据内积的公式进行计算;而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果。回忆刚才提到的映射的维度爆炸,在前一种方法已经无法计算的情况下,后一种方法却依旧能从容处理,甚至是无穷维度的情况也没有问题。
我们把这里的计算两个向量在映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ,例如,在刚才的例子中,我们的核函数为:
$$\kappa(x_1,x_2)=\left(\langle x_1, x_2\rangle + 1\right)^2$$
核函数能简化映射空间中的内积运算——刚好“碰巧”的是,在我们的 SVM 里需要计算的地方数据向量总是以内积的形式出现的。对比刚才我们写出来的式子,现在我们的分类函数为:
$$\sum_{i=1}^n\alpha_i y_i \color{red}{\kappa(x_i,x)} + b$$
其中\(\alpha\)由如下 dual 问题计算而得:
$$ \begin{align} \[ \max_\alpha \] &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j \color{red}{\kappa(x_i, x_j)} \\ s.t., &\alpha_i \geq 0, i=1,\ldots,n \\ &\sum_{i=1}^n\alpha_iy_i = 0 \end{align} $$
这样一来计算的问题就算解决了,避开了直接在高维空间中进行计算,而结果却是等价的,实在是一件非常美妙的事情!当然,因为我们这里的例子非常简单,所以我可以手工构造出对应于\(\varphi(\cdot)\)的核函数出来,如果对于任意一个映射,想要构造出对应的核函数就很困难了。
最理想的情况下,我们希望知道数据的具体形状和分布,从而得到一个刚好可以将数据映射成线性可分的\(\phi(\cdot)\),然后通过这个\(\phi(\cdot)\)得出对应的\(\kappa(\cdot,\cdot)\)进行内积计算。然而,第二步通常是非常困难甚至完全没法做的。不过,由于第一步也是几乎无法做到,因为对于任意的数据分析其形状找到合适的映射本身就不是什么容易的事情,所以,人们通常都是“胡乱”选择映射的,所以,根本没有必要精确地找出对应于映射的那个核函数,而只需要“胡乱”选择一个核函数即可——我们知道它对应了某个映射,虽然我们不知道这个映射具体是什么。由于我们的计算只需要核函数即可,所以我们也并不关心也没有必要求出所对应的映射的具体形式。 :slignt_smile:
当然,说是“胡乱”选择,其实是夸张的说法,因为并不是任意的二元函数都可以作为核函数,所以除非某些特殊的应用中可能会构造一些特殊的核(例如用于文本分析的文本核,注意其实使用了 Kernel 进行计算之后,其实完全可以去掉原始空间是一个向量空间的假设了,只要核函数支持,原始数据可以是任意的“对象”——比如文本字符串),通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:
- 多项式核
\(\kappa(x_1,x_2) = \left(\langle x_1,x_2\rangle + R\right)^d\),显然刚才我们举的例子是这里多项式核的一个特例(\(R=1,d=2\))。虽然比较麻烦,而且没有必要,不过这个核所对应的映射实际上是可以写出来的,该空间的维度是\(\binom{m+d}{d}\),其中\(m\)是原始空间的维度。 - 高斯核
\(\kappa(x_1,x_2) = \exp\left(-\frac{\|x_1-x_2\|^2}{2\sigma^2}\right)\),这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过,如果\(\sigma\)选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果\(\sigma\)选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数 $\sigma$ ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。 - 线性核
\(\kappa(x_1,x_2) = \langle x_1,x_2\rangle\),这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了。
最后,总结一下:对于非线性的情况,SVM 的处理方法是选择一个核函数\(\kappa(\cdot,\cdot)\),通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了 SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。
此外,略微提一下,也有不少工作试图自动构造专门针对特定数据的分布结构的核函数,感兴趣的同学可以参考,比如 NIPS 2003 的 Cluster Kernels for Semi-Supervised Learning 和 ICML 2005 的 Beyond the point cloud: from transductive to semi-supervised learning 等。


发表/查看评论