原文链接请点击这里
在最开始讨论支持向量机的时候,我们就假定,数据是线性可分的,亦即我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据,使用 Kernel 方法对原来的线性 SVM 进行了推广,使得非线性的的情况也能处理。虽然通过映射\(\phi(\cdot)\)将原始数据映射到高维空间之后,能够线性分隔的概率大大增加,但是对于某些情况还是很难处理。例如可能并不是因为数据本身是非线性结构的,而只是因为数据有噪音。对于这种偏离正常位置很远的数据点,我们称之为 outlier ,在我们原来的 SVM 模型里,outlier 的存在有可能造成很大的影响,因为超平面本身就是只有少数几个 support vector 组成的,如果这些 support vector 里又存在 outlier 的话,其影响就很大了。
例如下图:
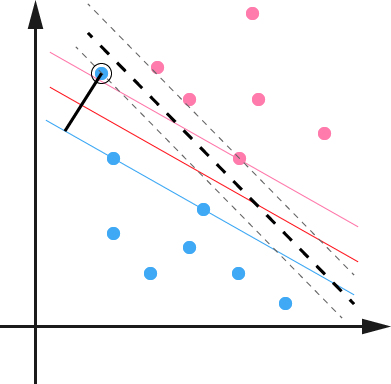
用黑圈圈起来的那个蓝点是一个 outlier ,它偏离了自己原本所应该在的那个半空间,如果直接忽略掉它的话,原来的分隔超平面还是挺好的,但是由于这个 outlier 的出现,导致分隔超平面不得不被挤歪了,变成途中黑色虚线所示(这只是一个示意图,并没有严格计算精确坐标),同时 margin 也相应变小了。当然,更严重的情况是,如果这个 outlier 再往右上移动一些距离的话,我们将无法构造出能将数据分开的超平面来。
为了处理这种情况,SVM 允许数据点在一定程度上偏离一下超平面。例如上图中,黑色实线所对应的距离,就是该 outlier 偏离的距离,如果把它移动回来,就刚好落在原来的超平面上,而不会使得超平面发生变形了。具体来说,原来的约束条件
$$y_i(w^Tx_i+b) \geq 1, \quad i=1,\ldots,n$$
现在变成
$$y_i(w^Tx_i+b) \geq 1\color{red}{-\xi_i}, \quad i=1,\ldots,n$$
其中\(\xi_i \geq 0\)称为松弛变量 (slack variable) ,对应数据点\(x_i\)允许偏离的 functional margin 的量。当然,如果我们允许\(\xi_i\)任意大的话,那任意的超平面都是符合条件的了。所以,我们在原来的目标函数后面加上一项,使得这些\(\xi_i\)的总和也要最小:
$$\min \frac{1}{2}\|w\|^2\color{red}{+C\sum_{i=1}^n \xi_i}$$
其中\(C\)是一个参数,用于控制目标函数中两项(“寻找 margin 最大的超平面”和“保证数据点偏差量最小”)之间的权重。注意,其中\(\xi\)是需要优化的变量(之一),而\(C\)是一个事先确定好的常量。完整地写出来是这个样子:
$$ \begin{align} \min & \frac{1}{2}\|w\|^2 + C\sum_{i=1}^n\xi_i \\ s.t., & y_i(w^Tx_i+b) \geq 1-\xi_i, i=1,\ldots,n \\ & \xi_i \geq 0, i=1,\ldots,n \end{align} $$
用之前的方法将限制加入到目标函数中,得到如下问题:
$$ \mathcal{L}(w,b,\xi,\alpha,r)=\frac{1}{2}\|w\|^2 + C\sum_{i=1}^n\xi_i – \sum_{i=1}^n\alpha_i \left(y_i(w^Tx_i+b)-1+\xi_i\right) – \sum_{i=1}^n r_i\xi_i $$
分析方法和前面一样,转换为另一个问题之后,我们先让\(\mathcal{L}\)针对\(w\)、\(b\)和\(\xi\)最小化:
$$ \begin{align} \frac{\partial \mathcal{L}}{\partial w}=0 &\Rightarrow w=\sum_{i=1}^n \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}}{\partial b} = 0 &\Rightarrow \sum_{i=1}^n \alpha_i y_i = 0 \\ \frac{\partial \mathcal{L}}{\partial \xi_i} = 0 &\Rightarrow C-\alpha_i-r_i=0, \quad i=1,\ldots,n \end{align} $$
将\(w\)带回\(\mathcal{L}\)并化简,得到和原来一样的目标函数:
$$\[ \max_\alpha \] \sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle$$
不过,由于我们得到\(C-\alpha_i-r_i=0\),而又有\(r_i \geq 0\)(作为 Lagrange multiplier 的条件),因此有\(\alpha_i \leq C\),所以整个 dual 问题现在写作:
$$ \begin{align} \[ \max_\alpha \] &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle x_i,x_j\rangle \\ s.t., &0 \leq \alpha_i\leq C, i=1,\ldots,n \\ &\sum_{i=1}^n\alpha_iy_i = 0 \end{align} $$
和之前的结果对比一下,可以看到唯一的区别就是现在 dual variable\(\alpha\)多了一个上限\(C\)。而 Kernel 化的非线性形式也是一样的,只要把 \(\langle x_i,x_j \rangle\)换成\(\kappa(x_i,x_j)\)即可。这样一来,一个完整的,可以处理线性和非线性并能容忍噪音和 outliers 的支持向量机才终于介绍完毕了。 😄


发表/查看评论