一、开篇

数学爱好者们汇集在网络论坛上的一大乐事就是对各类和数学相关的事物评头论足、论资排辈。如果要评选历史上最伟大的数学家，就会有一大堆的粉丝围绕高斯、黎曼、牛顿、欧拉、阿基米德等一流人物展开口水战；如果要讨论最奇妙的数学常数，\(e, \pi, \phi=\frac{\sqrt{5}-1}{2} \) 肯定在候选队列中；如果要推举最美丽的数学公式，欧拉公式 \(e^{i\pi} + 1= 0 \) 与和式 \( 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} \) 常常被数学爱好者们提及；如果有人追问最神奇的数学函数是什么？ 这个问题自然又会变得极具争议，而我相信如下这个长相有点奇特的伽玛函数

$$ \Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt $$

一定会出现在候选队列中。

伽玛函数不是初等函数，而是用积分形式定义的超越函数，怎么看都让人觉得不如初等函数自然亲切。然而伽玛函数也被称为阶乘函数，高等数学会告诉我们一个基本结论：伽玛函数是阶乘的推广。通过分部积分的方法，容易证明这个函数具有如下的递归性质

$$\Gamma(x+1) = x \Gamma(x)$$

由此可以推导出，对于任意的自然数\(n\)

$$\Gamma(n) = (n-1)! $$

由于伽玛函数在整个实数轴上都有定义，于是可以看做阶乘概念在实数集上的延拓。

如果我们继续再学习一些数学，就会惊奇地发现这个具有神秘气质的伽玛函数真是才华横溢。她栖身于现代数学的各个分支，在微积分、概率论、偏微分方程、组合数学， 甚至是看起来八竿子打不着的数论当中，都起着重要的作用。 并且这个函数绝非数学家们凭空臆想的一个抽象玩具，它具有极高的实用价值，频繁现身于在现代科学尤其是物理学之中。

笔者对数学的涉猎很有限，主要是从概率统计中频繁地接触和学习这个函数，不过这个函数多年来一直都让我心存疑惑：

• 都说\(n!\)和伽玛函数是近亲，可是从相貌上这两个数学公式都差了十万八千里，历史上数学家们是如何找到这个奇特的函数的？
• 现代数学对伽玛函数的定义使它满足 \(\Gamma(n) = (n-1)!\)，既然号称是\(n!\) 的推广，为何定义伽玛函数的时候不让它满足\(\Gamma(n) = n!\)？这看起来不是更加舒服自然吗？
• 伽玛函数是唯一满足阶乘特性的推广函数吗？
• 伽玛函数在各种概率分布的密度函数中频繁出现，伽玛函数本身是否有直观的概率解释？

带着这些疑问，笔者翻阅了许多讲解伽马函数历史和应用的资料，发现伽玛函数真是一个来自异族的美女，与生俱来携带着一种神秘的色彩。你要接近她并不难，然而她魅力独特，令你无法看透。从她出生开始，就吸引着众多一流的数学家对她进行解读。 历史上伽玛函数的发现，和数学家们对阶乘、插值以及积分的研究有着紧密的关系，而这最早要从著名的沃利斯公式讲起。

二、无心插柳——沃利斯公式

1655年, 英国数学家沃利斯(John Wallis, 1616-1703)写下了一个神奇的数学公式

\begin{equation} \label{wallis-formula} \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdot \cdots = \frac{\pi}{2} . \tag{2.1} \end{equation}

\(\pi\) 居然可以如此齐整地表示成奇数、偶数的比值，着实令人惊讶。 历史上数学家们为了寻求对\(\pi\) 这个迷人的常数更加深刻的理解，前赴后继倾注了无数的精力。数学家们发现，\(\pi\)可以表达成许许多多奇妙的形式，而沃利斯公式是欧洲历史上发现的第二个把\(\pi\) 表达成式了无穷序列的形式， 由于它简洁的对称美，也成为了许多数学人经常提及的数学公式之一。为何沃利斯公式会和伽玛函数发生联系呢？实际上对沃利斯公式做一下变形整理就可以得到如下等价形式

$$ \lim_{n\rightarrow\infty} \frac{(2^n \cdot n!)^4}{[(2n)!]^2(2n+1)} = \frac{\pi}{2} $$

我们看到了阶乘，所以沃利斯公式天然和阶乘有着紧密的联系。

我们先来欣赏一下沃利斯公式的证明。利用现代数学分析的知识证明这个公式并不难，通常微积分课本对这个公式的证明是从积分式

$$ I(n) = \int_0^\pi \sin^nxdx $$

出发，通过分部积分得到一个关于\(I(n)\)的递推公式，反复使用这个递推公式就可以证明结论。 不过这个证明思路有点繁琐，数学家波利亚(George P'{o}lya, 1887-1985) 在它的名著《数学与合情推理》中提到了另外一个非常简洁、符合直觉，但是不够严格的证明思路，其中用到的最重要的公式是数学家欧拉(Leonhard Euler, 1707-1783)提供的。欧拉当年研究正弦函数 \(\sin x\)的时候，发现该函数有无穷多个零点 \(0, \pm\pi, \pm 2\pi, \pm 3\pi, \cdots \)。 而一个多项式\(f(x)\) 如果有零点 \(x_1, x_2, \cdots, x_n\)(此处\(x_i, x_j\) 可以相同, 对应于有重根的情形), 那么 \(f(x)\) 一定可以表示为

$$ f(x) = a_0 (x-x_1) (x-x_2) \cdots (x-x_n) .$$

于是欧拉大胆地猜测 \(\sin x\)也具有多项式的这种性质，即

\begin{equation} \label{euler-sinx} \sin x = x \prod_{n=1}^\infty\left(1-\frac{x^2}{n^2\pi^2}\right) = x (1- \frac{x^2}{\pi^2}) (1- \frac{x^2}{4\pi^2}) (1- \frac{x^2}{9\pi^2}) \cdots . \tag{2.2} \end{equation}

理工科背景的学生大都学习过 \(\sin x\)的泰勒展开式， 通常只有数学背景的学生才会接触到这个 \(\sin x\) 的无穷乘积展开式。这个展开式在数学推导中有许多妙用。数学史上它发挥的第一个重要作用，就是帮助欧拉推导出了如下美丽的公式

$$ 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} . $$

这个展开式子的另一个妙处就是可以用于证明沃利斯公式， 不过这个思路并非欧拉本人给出，而是后来的数学家发现的。 在\(\eqref{euler-sinx} \)式中取 \(x=\frac{\pi}{2}\), 可以得到

$$ 1 = \frac{\pi}{2} \prod_{n=1}^\infty\left(1-\frac{1}{4n^2}\right) = \frac{\pi}{2} \prod_{n=1}^\infty\left(\frac{2n-1}{2n} \cdot \frac{2n+1}{2n}\right) $$

所以

$$ \frac{\pi}{2} = \prod_{n=1}^\infty\left(\frac{2n}{2n-1} \cdot \frac{2n}{2n+1}\right) $$

上式就是沃利斯公式。之所以说以上的证明思路不够严格，是由于欧拉给的\(\sin x\) 无穷乘积展开式的严格证明并不简单，依赖于现代数学分析理论。

欣赏完沃利斯公式的证明，我们把镜头重新拉回到沃利斯生活的年代，要知道沃利斯给出这个公式是在 1655 年，那时候牛顿刚满13岁，莱布尼茨更小，欧拉还没出生，整个欧洲数学界对微积分的认识还停留在非常粗糙的阶段，对正弦函数 \(\sin x\) 的认识也非常有限， 所以沃利斯当然不可能用上述的思路找到他的公式， 那沃利斯是如何发现这个 \(\pi\)的无穷乘积表达式的呢？

在沃利斯的时代，微积分有了初步的进展，当时考虑的典型的问题就是求一个曲线和坐标轴围成的面积。欧洲的数学家们追寻阿基米德一千多年前开创的穷竭法，把曲线下的面积表达为求无穷多个矩形面积的和。当积分的思想在十七世纪开始逐步发酵的时候，沃利斯已经能够运用积分的思路处理一些简单曲线的面积。譬如，对于最简单的幂函数曲线 \(y=x^n\)，使用我们现在的数学记号， 沃利斯时代的数学家们获得了如下的结果

$$ \int_0^1 x^n dx = \frac{1}{n+1}, n=0,1,2,\ldots .$$

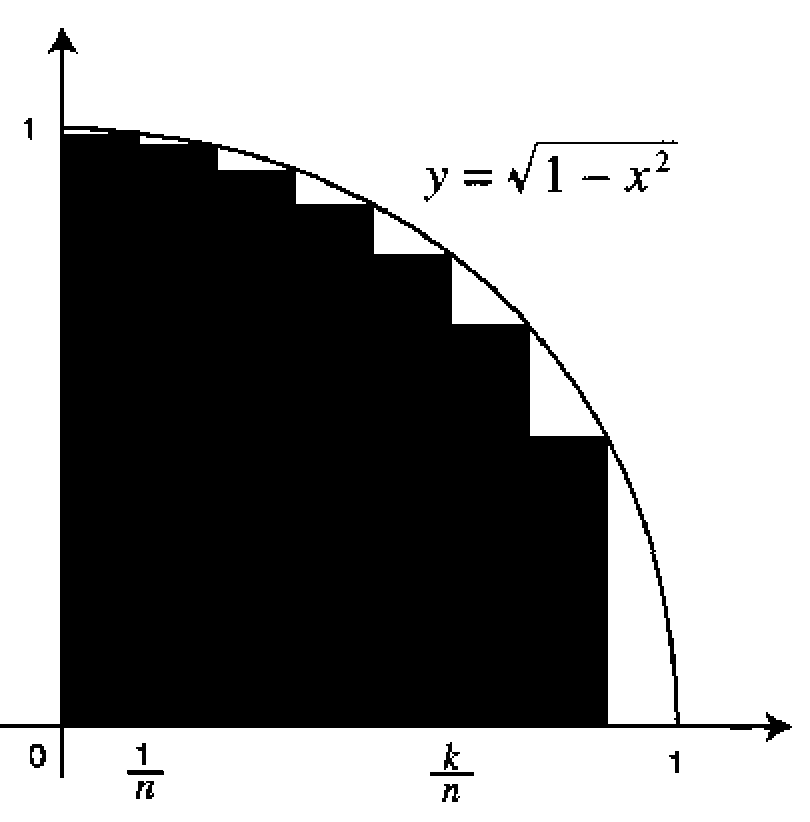
圆的面积一直是千百年来数学家们深入关心和研究的问题，很自然地沃利斯也想到了可以使用同样的思路来处理圆的面积。 不过数学家们早已经证明道圆的面积是 \(\pi r^2\)，用积分的方法去计算圆的面积能带来什么好处呢？ 沃利斯在此做了一个逆向思维，他的真实目标并不是要计算圆的面积，而是冲着\(\pi\) 去的。 沃利斯的一个漂亮的思路是：我们已经知道四分之一的单位圆圆弧 \(y=\sqrt{1-x^2} (0 \le x \le 1)\) 和坐标轴围成的面积是 \(\frac{\pi}{4}\), 如果这个面积能通过无穷分割的方法表达成一个解析表达式，那我们其实就可以得到计算 \(\pi\) 的一个解析表达式。

然而沃利斯在处理这个圆弧下地面积的时候遇到了困难。虽然基于无穷分割的方法可以得到

$$ \int_0^1 (1-x^2)^{1/2} dx = \lim_{n\rightarrow \infty} \frac{1}{n} \sum^n_{k=1} \sqrt{1-\frac{k^2}{n^2}}$$

但是这个极限难以简化计算。 沃利斯天才的地方就是换了一个更一般的思路来处理这个问题：

• 考虑更一般的曲线面积问题 $$ A_{p,q} = \int_0^1 (1-x^\frac{1}{p})^q dx$$ 原来的问题变成了一个特例，就是计算 \(A_{\frac{1}{2},\frac{1}{2}}\)
• 对\(p,q\)为整数的情况做计算，并系统地列成表格， 从表格中观察变化规律，总结出一般的公式；
• 把计算公式从\(p,q\)为整数的情形延拓、内插到分数的情形，从而计算出\(A_{\frac{1}{2},\frac{1}{2}}\)

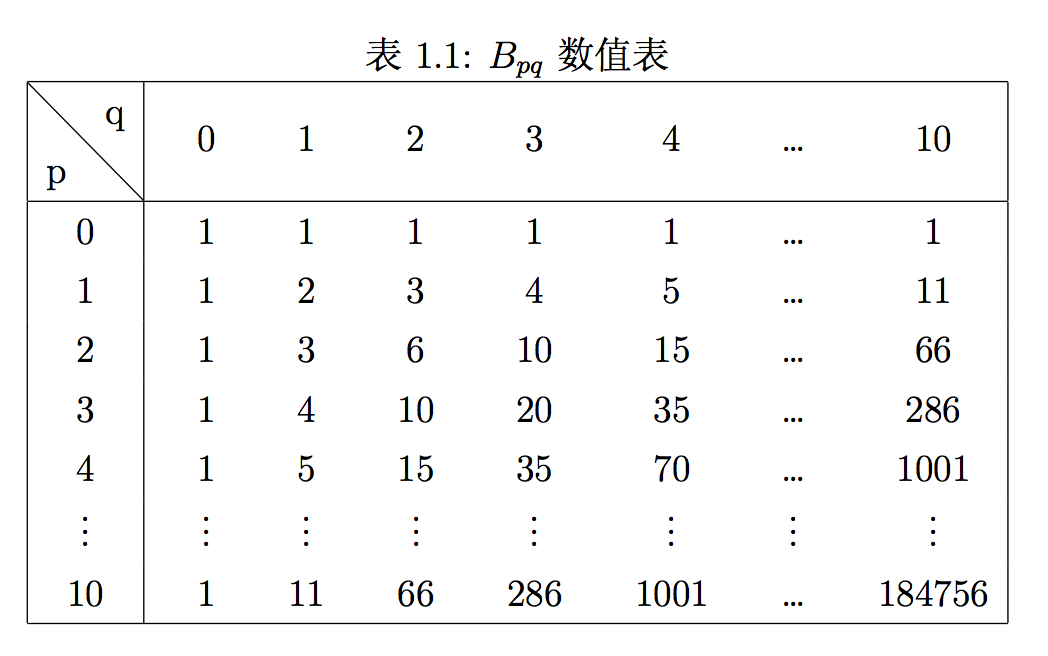
沃利斯对 \(p,q = 1,2,\ldots,10\) 做了计算， 发现\(A_{p,q}\)这个表格不太好看，改为倒数之后容易分析。于是取 \(B_{p,q} = \frac{1}{A_{p,q}}\), 列出表格一看， 居然恰好是帕斯卡三角形！ 这个三角形中的组合数已经是数学家们熟悉知的， 于是沃利斯很容易地得到

\begin{equation} \label{wallis-Bpq} B_{p,q} = \frac{(p+q)!} {p! q!} = \frac{1}{p!} (q+1) (q+2) \ldots (q+p), q=0,1,2 \ldots \tag{2.3} \end{equation}

由上式进一步可以得到如下的递推公式

\begin{equation} \label{wallis-Bpq-recursion} B_{p,q} = \frac{p+q}{q} B_{p,q-1} \tag{2.4} \end{equation}

原始的问题就转化为计算 \(B_{\frac{1}{2},\frac{1}{2}}\)。 由此开始， 沃利斯开始了他天才的推广：

• 虽然 \eqref{wallis-Bpq} 和 \eqref{wallis-Bpq-recursion} 是基于\(p,q\)为整数得到的， 但是沃利斯认为这个公式也应该适用于分数的情形；
• 由于原始表格是对称的， 沃利斯相信推广到分数之后的表格依然保持对称性。

基于对称性假设和计算式 \eqref{wallis-Bpq}, 我们可以得到，

$$ B_{\frac{1}{2}, 1} = B_{1, \frac{1}{2}} = \frac{1}{1!}(\frac{1}{2} + 1) = \frac{3}{2} $$

考虑 \(p=\frac{1}{2}\) 的情形, 重复使用迭代公式 \eqref{wallis-Bpq}, 容易得到

$$ B_{\frac{1}{2}, m} = \frac{2m+1}{2m}\cdot \frac{2m-1}{2m-2} \ldots \frac{5}{4} \cdot\frac{3}{2} $$

$$ B_{\frac{1}{2}, m+\frac{1}{2}} = \frac{2m+2}{2m+1} \cdot\frac{2m}{2m-1} \ldots \frac{4}{3} \cdot B_{\frac{1}{2}, \frac{1}{2}} $$

由于 \(B_{\frac{1}{2}, q}\) 是基于\(q\)递增的，所以有

$$ B_{\frac{1}{2}, m-\frac{1}{2}} < B_{\frac{1}{2}, m} < B_{\frac{1}{2}, m+\frac{1}{2}} $$

利用 \eqref{wallis-Bpq-recursion} 式这个递推公式，马上可以得出上式两端有相同的极限

$$ \lim_{m \rightarrow \infty} B_{\frac{1}{2}, m+\frac{1}{2}} = \lim_{m \rightarrow \infty} \frac{2m+2}{2m+1} B_{\frac{1}{2}, m-\frac{1}{2}} = \lim_{m \rightarrow \infty} B_{\frac{1}{2}, m-\frac{1}{2}} . $$

于是，利用两侧极限的夹逼，可以得到

$$ \lim_{m \rightarrow \infty} B_{\frac{1}{2}, m} = \lim_{m \rightarrow \infty} B_{\frac{1}{2}, m+\frac{1}{2}} $$

即有

$$ \frac{3}{2} \cdot \frac{5}{4} \cdot \cdots \cdot \frac{2m-1}{2m-2} \cdot \frac{2m+1}{2m} \cdots = B_{\frac{1}{2}, \frac{1}{2}} \cdot \frac{4}{3} \cdot \cdots \cdot \frac{2m}{2m-1} \cdot \frac{2m+2}{2m+1} \cdot \cdots $$

所以

$$ \frac{2}{B_{\frac{1}{2}, \frac{1}{2}}} = \frac{2}{1} \cdot\frac{2}{3} \cdot\frac{4}{3}\cdot \frac{4}{5}\cdot \cdots \cdot \frac{2m-2}{2m-1}\cdot \frac{2m}{2m-1} \cdot \frac{2m}{2m+1} \cdot \frac{2m+2}{2m+1} \cdot\cdots $$

由于 \(\displaystyle \frac{2}{B_{\frac{1}{2}, \frac{1}{2}}} = 2A_{\frac{1}{2}, \frac{1}{2}} = \frac{\pi}{2} \),代入上式就得到了沃利斯公式 \eqref{wallis-formula}。

上述推导的基本思想是在沃利斯的名著《无穷分析》（Arithmetica Infinitorum，1655）中给出的。沃利斯公式对\(\pi\)的表示如此的奇特，以至于惠更斯第一次看见这个公式的时候根本不相信，直到有人给惠更斯展示了利用该公式对\(\pi\)做近似计算，才消除了惠更斯的疑惑。沃利斯是在牛顿之前英国最有影响力的数学家，他的这本书包含了现代微积分的先驱工作，给后来的数学家包括牛顿、斯特林、欧拉都产生了重要的影响。牛顿1642年在老家研读沃利斯的这本书的时候受到启发，从而把二项式定理从整数的情形推广到了分数的情形，这也是牛顿有生以来的第一个数学发现；而牛顿后续在微积分上的工作也同样受到了沃利斯的深刻影响。

回过头来我们观察一下沃利斯公式推导过程中使用的 \eqref{wallis-Bpq} 式，这个组合公式中实际上包含了阶乘\(p!\)、 \(q!\), 当沃利斯认为这个公式也适合于\(p, q\) 为分数的情形的时候，隐含了一个假设是阶乘这个源自整数的概念是可以推广到分数的情形的。虽然沃利斯并没有显示地提出把阶乘推广到分数的问题， 沃利斯对一些特殊积分式的研究、沃利斯公式的结论以及推导过程却给后来的数学家们进一步研究阶乘提供了许多重要的线索，也为未来伽玛函数的发现埋下了一颗种子。

三、近似与插值的艺术

十七世纪中期，由于帕斯卡、费马、贝努利等数学家的推动，概率论以及与之相关的组合数学获得了很大的发展，阶乘的数值计算开始频繁的出现在数学家面前。 真正的开始对 \(n!\)进行细致地研究并取得突破的，是数学家棣莫弗(Abraham de Moivre, 1667-1754)和斯特林(James Stirling, 1692-1770)。

棣莫弗从1721年开始考虑二项分布的概率计算问题，其中一个问题是：当\(n \rightarrow \infty \)时，如何计算对称二项分布的中间项的概率

$$ b\left(n, {1\over2}, {n \over 2}\right) = \binom{n}{{n \over 2}} \left(\frac{1}{2}\right)^n = \frac{n!}{({n\over 2})! \cdot ({n \over 2})!} \left(\frac{1}{2}\right)^n .$$

上式中假设了\(n\)为偶数。棣莫弗经过一番复杂的推导计算，得到了如下的结果

$$ b\left(n, {1\over2}, {n\over2}\right) \approx 2.168 \frac{(1-{1\over n})^n} {\sqrt{n-1}} \approx \frac{2.168 e^{-1}}{\sqrt{n}}.$$

1725年，斯特林得知了棣莫弗的研究问题和结果，这激起了他浓厚的兴趣。斯特林经过更细致的推导，得到了如下更加漂亮的结果

$$ b\left(n, {1\over2}, {n\over2}\right) \approx \sqrt{\frac{2}{\pi n}} .$$

斯特林写信告知了棣莫弗他的推导结果，斯特林的结果中最引人注目的地方就是 \(\pi\) 的引入，这给棣莫弗很大的启发。 基于上述二项概率计算的研究，棣莫弗最终给出了如下重要公式

$$ n! \approx C \sqrt{n} \left(\frac{n}{e}\right)^{n} $$

\(C\)是一个常数。而在斯特林推导\(b(n, {1\over2}, {n\over2})\)过程中引入 \(\pi\)的启发下， 1730 年棣莫弗利用沃利斯公式推导出了 \(C = \sqrt{2\pi}\)，也就是得到了斯特林公式

$$ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^{n} .$$

所以现代数学史的研究大都认为斯特林公式的最主要贡献者是棣莫弗，斯特林的贡献主要在常数\(C\)的确定。 不过科学发展史中长期以来都存在一个被称之为 Stigler’s Law 的著名现象：绝大多数科学成果的冠名，大都不是历史上首位发现者的名字。或许这主要是由于早年通信不发达、信息传播成本太高导致的。如今互联网如此的发达，学术界任何重要的科研进展都可以快速传导到世界各地，这种问题发生的概率大大的降低了，类似牛顿、莱布尼茨这种微积分发明权的世纪争夺战不太可能在这个时代重现。

斯特林公式自发现以来，就吸引众多的数学家对它进行研究，提出了多种多样的证明方法。实际上，从沃利斯公式出发就可以证明斯特林公式，甚至可以进一步证明斯特林公式和沃利斯公式是完全等价的。在多种证明方法中，有一个基于概率论的证明思路：利用泊松分布的特性，再加上中心极限定理，我们可以简洁地推导出斯特林公式。

假设 \(X_1, X_2,\ldots, X_n\)独立同分布， 都是服从参数 \(\lambda=1\) 的泊松分布的随机变量，取 \(S_n=\sum_{i=1}^n X_i\), 则由泊松分布的可叠加性， 容易知道 \(S_n \sim Poisson(n)\), 于是由泊松分布的性质可知\(S_n\) 的均值和方差都是 \(n\), 利用中心极限定理可以得到

$$ Z_n = \frac{S_n-E(S_n)}{\sqrt{ Var(S_n) }} = \frac{S_n-n}{{\sqrt n }} \rightarrow Z, \quad Z \sim N(0,1) $$

\(Z\)为正态分布随机变量，密度函数为

$$ \displaystyle f(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}} .$$

所以，我们有如下推导

\begin{eqnarray*} \begin{array}{lll} P\{{S_n} = n\} & = & \displaystyle P\{ n -1 < {S_n} \le n\} \\ & = & \displaystyle P\{ -\frac{1}{{\sqrt n }} < \frac{{{S_n} -n}}{{\sqrt n }} \le 0\} \\ & \approx & \displaystyle P\{ -\frac{1}{{\sqrt n }} < Z \le 0\} \\ & = & \displaystyle \int_{ -\frac{1}{{\sqrt n }}}^0 f(z) dz \\ & \approx & f(0) [0 -( -\frac{1}{{\sqrt n }})] \\ & = & \displaystyle \frac{1}{\sqrt{2\pi n}} .\\ \end{array} \end{eqnarray*}

由于\(S_n\) 符合参数\(\lambda =n\)的泊松分布，实际上有

$$ P\{ {S_n} = n\} = \frac{{{e^{ -n}}{n^n}}}{{n!}} .$$

综合以上推导可以得到

$$ \frac{{{e^{ -n}}{n^n}}}{{n!}} \approx \frac{1}{\sqrt{2\pi n}}. $$

上式稍微整理一下就得到斯特林公式。这个推导的思路看起来非常初等，但是由于中心极限定理的严格证明非常困难，所以不能被认为是一个严格的初等证明。不过该推导让我们从概率角度来理解斯特林公式，同时也解释了斯特林公式中的\(\pi\)，是由于正态分布的引入导致的。

斯特林公式非常有用，通过它可以得出\(n!\) 非常精确的估计值。虽然\(n\) 足够大时绝对误差可以超过任何数，但是相对误差却很小，并且下降得非常快，甚至当\(n!\) 很小的时候，斯特林公式的逼近都相当精确。

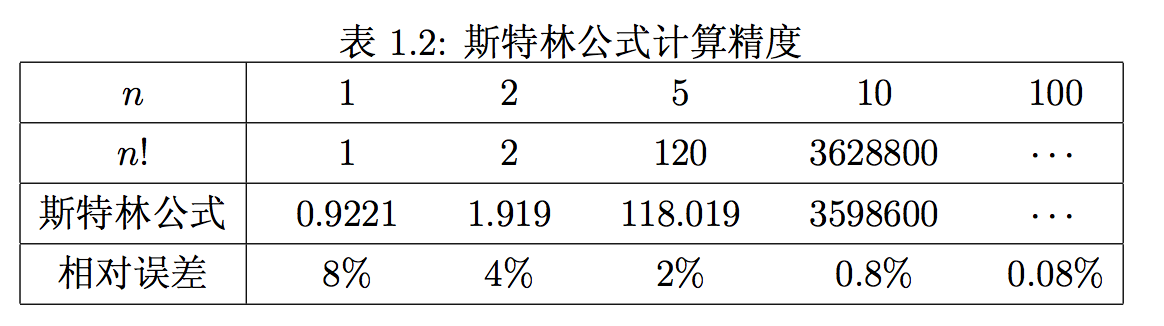
不过，斯特林对于 \(n!\) 的研究实际上走得更远，而不是仅限于近似计算。追寻沃利斯和牛顿在插值方面的工作，斯特林一直研究各种数列的插值问题，通俗地说就是把数列的通项公式定义从整数集合延拓到实数集合。例如数列 \(1,4,9,16,\cdots\) 可以用通项公式 \(n^2\) 自然的表达，即便 \(n\)为实数，这个通项公式也是良定义的。直观地说就是可以找到一条通过所有整数点\((n,n^2)\)的平滑曲线\(y=x^2\)，从而可以把定义在整数集上的公式延拓到实数集合。再比如求和序列 \(1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5 \cdots\), 其通项公式可以写为 \(n(n+1)/2\) ，这个公式也可以很容易地延拓到实数集合上。 斯特林很擅长于处理各种序列的插值问题，他在1730 年出版的一本书中描述了很多基于多阶差分处理序列插值的方法，这些方法主要源自牛顿。 斯特林处理插值的思路稍微有点复杂，我们不在此赘述，他的方法本质上类似于使用多项式曲线做插值。我们知道平面上两个点可以确定一条直线，三个点可以确定一条抛物线，…，\(n\)+1 个点可以确定一条\(n\)次多项式曲线。所以对于一个整数序列，如果我们无法直观地写出通项公式，为了计算某一个实数点对应的值，可以用该实数点周围的 \(n+1\)个整数点去确定一条 \(n\) 次多项式曲线，从而可以基于拟合得到的多项式近似地计算实数点的值。

自然数的加法序列我们已经看到很容易做插值计算，对数学家们而言很自然的一个问题就是：自然数的乘法序列 \(1,1\cdot2, 1\cdot2\cdot3, 1\cdot2\cdot3\cdot4, 1\cdot2\cdot3\cdot4\cdot5, \cdots\) 能否做插值计算？我们可以计算 \(2!,3!\), 如何计算 \((\frac{1}{2})!\)呢？斯特林在他的书中开始考虑阶乘序列\(1!, 2!,3!,4!,5! \cdots\)的插值问题。 如果我们把\((n,n!)\)最初的一些点画在坐标轴上，确实可以看到，容易画出一条通过这些点的平滑曲线。

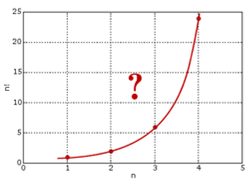
但是\(n!\)这个数列增长的速度过快，数值计算非常困难，要做这个序列的插值计算可不容易。幸运的是当时对数已经被纳皮尔(John Napier, 1550-1617) 发明出来，并且在数值计算上显示了其神通，被科学家们广泛接受。斯特林和棣莫弗在他们的研究中大量的使用对数做计算，所以很自然地斯特林转而考虑对序列 \(\log_{10} n!\) 做插值计算。

通过插值方法并结合对数运算的技巧，斯特林计算出了 \(\log_{10} (10\frac{1}{2})!=7.0755259056\), 由此可以得到 \((10\frac{1}{2})! = 11899423.08\)。斯特林接下来的处理非常有意思，由于原始的数列满足递归式 \(T(z) = z \cdot T(z-1)\)，所以斯特林基于插值的原则进行推理，认为被插值的中间项 \((\frac{1}{2})!, (1\frac{1}{2})!, (2\frac{1}{2})! \cdots\),\((9\frac{1}{2})!, (10\frac{1}{2})!\)也应该满足这个递归式, 于是有

$$ \left(10\frac{1}{2}\right)! = 10\frac{1}{2} \cdot 9\frac{1}{2} \cdot \cdots \cdot 1\frac{1}{2} \cdot \left(\frac{1}{2}\right)! $$

上式中代入\((10\frac{1}{2})!\)的值，很容易计算得到

$$\left(\frac{1}{2}\right)! = 0.8862269251 .$$

这个结果看起来平淡无奇，然而斯特林天才地指出实际上有

\begin{equation} \label{half-factorial} \left(\frac{1}{2}\right)! = \frac{\sqrt\pi}{2} . \tag{2.5} \end{equation}

这真是一个令人惊诧的结果！

我们不太确定斯特林是如何推断出 \eqref{half-factorial} 式的，因为在斯特林的论述中他只是把 \((\frac{1}{2})!\) 计算的结果和 \(\frac{\sqrt\pi}{2}\)做了数值比较，并没有进行严谨的数学推导，所以看起来好像是数值对比后猜测的结果。即便如此，这也展示了斯特林强大的数学直觉。

然而考虑到我们熟悉的斯特林公式是斯特林和棣莫弗共同创造的，斯特林要利用他的插值过程更加严谨地推导这个结果其实也很容易，虽然没有证据表明斯特林做过这种推导。基于斯特林对 \(\log_{10} n!\)的插值处理方法，如果我们只是使用一次多项式（即直线）做插值处理，那么中间项的插值就是两端的算术平均

$$ \log_{10} \left(n+\frac{1}{2}\right)! = \frac{\log_{10} n! + \log_{10} (n+1)!}{2} .$$

所以

$$ \left(n+\frac{1}{2}\right)! = \sqrt{n! (n+1)!} = n! \sqrt{n+1} ,$$

把递归式 \(T(z) = z \cdot T(z-1)\) 应用于 \((n+\frac{1}{2})!\) 可以得到

$$ \left(n+\frac{1}{2}\right)! = (n+\frac{1}{2}) \cdot (n-\frac{1}{2}) \cdots \frac{3}{2} \cdot \left(\frac{1}{2}\right)! .$$

利用斯特林公式推导可以得到

\begin{align*} \left(\frac{1}{2}\right)! & = \frac {n! \sqrt{n+1}} {(n+\frac{1}{2}) \cdot (n-\frac{1}{2}) \cdots \frac{3}{2}} \\ & = \frac {\sqrt{n+1} \cdot 2^{2n} \cdot n! \cdot n!} {(2n+1)!} \\ & \displaystyle \approx \displaystyle \frac {\sqrt{n+1} \cdot 2^{2n} \cdot \sqrt{2\pi n} (\frac{n}{e})^n \cdot \sqrt{2\pi n} (\frac{n}{e})^n} {\sqrt{2\pi(2n+1)} (\frac{2n+1}{e})^{2n+1}} \\ & = \displaystyle \frac{\sqrt\pi}{2} \cdot \frac{e}{(1+\frac{1}{2n})^{2n}} \cdot \frac{\sqrt{2n+2}\cdot 2n}{\sqrt{2n+1}\cdot (2n+1)} \\ & \rightarrow \frac{\sqrt\pi}{2} \hspace{0.5cm} (n \rightarrow \infty) . \end{align*}

斯特林的插值研究成果发表于他1730年出版的《Methodus Differentialis》中，由于原书是拉丁文写成的，有人把他翻译成了英文，并对斯特林的研究成果提供了很多的评论，使得我们有机会追寻斯特林研究的原始足迹。 有了强大的斯特林公式，可以对\(n!\) 进行便捷的近似计算， 而事实上按照斯特林的插值思路，他已经可以近似计算\(n\)为任何分数的时候的阶乘。然而斯特林的思路更多只是停留在数值近似计算上，没有把 \(n!\) 到分数的延拓更细致地追究下去。

四、三封信——伽玛函数的诞生

和斯特林处在同一个时代的另外一位数学家几乎在同一个时间点也在考虑\(n!\)的插值问题，这个人就是哥德巴赫。哥德巴赫的名字在中国真是家喻户晓。由于中国数学家在数论领域的杰出成就，和素数相关的哥德巴赫猜想作为数学皇冠上的明珠就一直吸引着无数中国人的目光。 哥德巴赫一生都对数列的插值问题保持浓厚的兴趣，他很早就开始考虑阶乘的插值问题。不过看起来哥德巴赫的思路不同于斯特林，他并不满足于仅仅做近似的数值计算，他希望能找到一个通项公式，既可以准确的描述\(n!\), 又能够同时推广到分数情形。不过哥德巴赫无法解决这个问题，幸运的是哥德巴赫交友广泛，和当时许多著名的数学家都有联系，包括莱布尼茨以及数学史中出了最多位数学家的家族–贝努利家族。1722 年他找尼古拉斯·贝努利请教这个阶乘插值问题，不过没有取得任何进展。即便如此，哥德巴赫却多年来一直不忘思考这个问题，1729年他又请教尼古拉斯·贝努利的弟弟丹尼尔·贝努利，而丹尼尔于当年10月给哥德巴赫的一封信中给出了漂亮的解答。

丹尼尔解决阶乘插值问题的思路非常漂亮：突破有限，取道无穷！他不拘泥于有限的方式，而是直接跳跃到无穷乘积的形式做插值。丹尼尔发现，如果 \(m,n\)都是正整数，当 \(m \rightarrow \infty\)时，有

$$ \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m-1+n)}(m+\frac{n}{2})^{n-1} \rightarrow n! .$$

于是利用这个无穷乘积的方式可以把\(n!\)的定义自然地延拓到实数集。例如，取 \(n=2.5\), \(m\)足够大，基于上式就可以近似计算出 \(2.5!\)。我们并不知道丹尼尔是如何想到用无穷乘积的思路去解决这个问题的，然而他能从有限插值跳跃到无穷，足以显示他优秀的数学才能。无穷在整个数学发展中发挥着巨大的作用，二十世纪之后的数学笔者不敢妄加评论，然而如果说“无穷是数学发展的发动机”，在二十世纪之前，这句评论应该不会过分。历次数学危机是因为无穷而产生，几次数学的重大进展和飞跃也是由于数学家们更加深刻地认识了无穷。

接下来伽马函数的主角欧拉要登场了。欧拉和贝努利家族有紧密的联系，他是约翰·贝努利 (Johann Bernoulli, 1667-1748)的学生， 这位约翰也就是尼古拉斯和丹尼尔的父亲。我们应该感谢约翰·贝努利，因为正是他发现并培养了欧拉的数学才能。 在尼古拉斯和丹尼尔的推荐之下欧拉于1727年在圣彼得堡科学院获得了一个职位。欧拉当时正和丹尼尔·贝努利一块在圣彼得堡，他也因此得知了阶乘的插值问题。应该是受到丹尼尔·贝努利的思路的启发，欧拉也采用无穷乘积的方式给出了另外一个\(n!\) 的插值公式

\begin{equation} \label{euler-series} \Bigl[\Bigl(\frac{2}{1}\Bigr)^n\frac{1}{n+1}\Bigr] \Bigl[\Bigl(\frac{3}{2}\Bigr)^n\frac{2}{n+2}\Bigr] \Bigl[\Bigl(\frac{4}{3}\Bigr)^n\frac{3}{n+3}\Bigr] \cdots = n! . \tag{2.6} \end{equation}

用极限形式，这个式子以写为

\begin{equation} \label{euler-series2} \lim_{m \rightarrow \infty} \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} = n! \tag{2.7} \end{equation}

欧拉实际上在他的论文中描述了发现上述式子的思路，我们不在此赘述，不过上式成立却很容易证明。上式左边可以整理为

$$ \begin{align*} & \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} \\ = & \frac{1\cdot 2\cdot 3 \cdots n \cdot (n+1)(n+2) \cdots m}{(1+n)(2+n)\cdots m (m+1)(m+2)\cdots (m+n)} (m+1)^{n} \\ = & 1\cdot 2\cdot 3 \cdots n \cdot \frac{(n+1)(n+2) \cdots m}{(1+n)(2+n)\cdots m } \cdot \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\ = & n! \cdot \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\ = & n! \cdot \prod_{k=1}^{n} \frac{m+1}{m+k} \\ \rightarrow & n! \qquad (m\rightarrow \infty) \end{align*} \tag{1.1} $$

所以 \eqref{euler-series}、\eqref{euler-series2}式都成立。

而由于 \eqref{euler-series} 式对于\(n\)为分数的情形也适用，所以欧拉实际上也把\(n!\) 的计算推广到了分数的情形，只是这个计算是用无穷乘积的形式表示的，看起来不够直观。欧拉给的无穷乘积相比丹尼尔的无穷乘积有什么更出色的地方吗？实际上后人的验证指出，就收敛到\(n!\)的速度而言，丹尼尔的无穷乘积比欧拉的要快得多，然而欧拉的无穷乘积公式却是能够下金蛋的。 欧拉尝试从一些简单的例子开始做计算，看看是否有规律可循，欧拉极其擅长数学的观察与归纳。当 \(n=\frac{1}{2}\)的时候，带入 \eqref{euler-series} 式，可以得到

\begin{align*} \left(\frac{1}{2}\right)! = & \sqrt{\frac{2}{1}} \cdot \frac{2}{3} \cdot \sqrt{\frac{3}{2}} \cdot \frac{4}{5} \cdot \sqrt{\frac{4}{3}} \cdot \frac{6}{7} \cdot \sqrt{\frac{5}{4}} \cdot \frac{8}{9} \cdot \cdots \\ = & \sqrt{\frac{4}{2}} \cdot \frac{2}{3} \cdot \sqrt{\frac{6}{4}} \cdot \frac{4}{5} \cdot \sqrt{\frac{8}{6}} \cdot \frac{6}{7} \cdot \sqrt{\frac{10}{8}} \cdot \frac{8}{9} \cdot \cdots \\ = & \sqrt{\frac{4}{3} \cdot \frac{2}{3}} \cdot \sqrt{\frac{6}{5} \cdot \frac{4}{5}} \cdot \sqrt{\frac{8}{7} \cdot \frac{6}{7}} \cdot \sqrt{\frac{10}{9} \cdot \frac{8}{9}} \cdot \cdots \\ = & \sqrt{\frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdot \frac{10}{9} \cdot \cdots } \end{align*}

对比一下根号内的式子和沃利斯公式 \eqref{wallis-formula}，几乎是一模一样，只是最前面差了一个因子2。 欧拉自然非常熟悉沃利斯的工作，基于沃利斯公式，欧拉迅速得到了如下一个令他惊讶的结果

$$ \Bigl(\frac{1}{2}\Bigr)! = \frac{\sqrt{\pi}}{2} .$$

欧拉给的无穷乘积满足阶乘的递归式\(T(z) = z T(z-1)\), 结合递归式和计算技巧欧拉还计算了其它几个分数，包括 \(\frac{5}{2}, \frac{1}{4}, \frac{3}{4}, \frac{1}{8}, \frac{3}{8} \) 等分数的阶乘。在丹尼尔的鼓励之下，欧拉把自己的插值公式以及一些分数阶乘的计算结果写信告知了哥德巴赫，这开启了欧拉和哥德巴赫之间一生的通信交流。两人在接下来的 35 年里连续通信达到196封，这些信函成为了数学家们研究欧拉的重要资料，而著名的哥德巴赫猜想就是首次出现在哥德巴赫写给欧拉的一封信中，也正是哥德巴赫激发了欧拉对数论的兴趣。

欧拉是具有超凡的数学直觉的数学家，他看到 \((\frac{1}{2})!\) 中居然有 \(\pi\), 对于擅长数学分析的数学家而言，有 \(\pi\) 的地方必然有和圆相关的积分。同时由于计算\( (\frac{1}{2})!\)过程中使用到的沃利斯公式，实际上也是计算积分的产物，由此欧拉猜测 \(n!\) 应该可以表达为积分形式，于是欧拉开始努力尝试把 \(n!\) 表达为某种积分。虽然沃利斯的时代微积分的系统理论还没有发明出来，沃利斯使用插值的方式做一些推导计算，但是沃利斯公式的推导过程本质上就是在处理积分。 如果说沃利斯当年只是无心插柳，那后继者欧拉是发现了一片绿洲。 受沃利斯工作的启发，欧拉开始考虑如下一般形式的积分

$$ J(e,n) = \int_0^1 x^e(1-x)^ndx$$

此处 \(n\) 为正整数，\(e\) 为正实数。利用分部积分法，很容易证明

$$ J(e,n) = \frac{n}{e+1}J(e+1,n-1) $$

重复使用上述迭代公式，最终可以得到

$$ J(e,n) = \frac{1\cdot2\cdots n}{(e+1)(e+2)\cdots(e+n+1)} $$

于是欧拉得到如下一个重要的式子

\begin{equation} n! = (e+1)(e+2)\cdots(e+n+1)\int_0^1 x^e(1-x)^ndx \tag{2.8} \end{equation}

在这个公式里欧拉实际上已经成功地把\(n!\)表示成了积分的形式。然而这里的问题是 \((e+1)(e+2)\cdots(e+n+1)\)这个表达式限制了 \(n\)只能为整数，无法推广到分数的情形，欧拉继续研究能否简化这个积分表达式。此处\(e\)是一个任意实数，有没有办法让\(e\)从上面的积分式子中消失呢？要让一个量从一个数学等式中消失，数学家们惯用的手法之一就是让这个量取一个极端的值，譬如无穷。欧拉的老师约翰·贝努利说过“无穷是上帝的属性”，在通往无穷的路途中，造物主的秘密往往被数学家们窥视。欧拉开始追问：如果让\(e\) 趋向于无穷取值，会发生什么样的情况呢？分析学的大师欧拉开始展现他的计算技巧，取\(e=\frac{f}{g}\), 稍微整理一下可以得到

$$ \frac{n!}{(f+g)(f+2g)\cdots(f+ng)} = \frac{f+(n+1)g}{g^{n+1}} \int_0^1 x^\frac{f}{g}(1-x)^n dx $$

然后令 \(f \rightarrow 1, g \rightarrow 0\)，显然上式左边趋于\(n!\), 右边会发生什么情况呢？为了简化计算，令 \(x=t^h, h=\frac{g}{f+g}\)， 整理之后上式可以变换为

\begin{align} \frac{n!}{(f+g)(f+2g)\cdots(f+ng)} & = \frac{f+(n+1)g}{g^{n+1}} \int_0^1 h(1-t^h)^n dt \notag \\ & = \frac{f+(n+1)g}{(f+g)^{n+1}} \int_0^1 \Bigl(\frac{1-t^h}{h}\Bigr)^n dt \label{factorial-integral} \tag{2.9} \end{align}

当\(f \rightarrow 1, g \rightarrow 0\)时显然有\(h \rightarrow 0\)，利用罗必塔法则，我们可以得到微积分中一个熟知的式子

$$ \lim_{h \rightarrow 0} \frac{1-t^h}{h} = -\log t .$$

于是对 \eqref{factorial-integral} 式两边取极限，奇迹出现了

\begin{equation} \label{factorial-gamma-1} n! = \int_0^1 (-\log t)^ndt, \tag{2.10} \end{equation}

原来的积分式中的\(e\)消失了，欧拉成功地把\(n!\)表达为了一个非常简洁的积分形式！！！对上式再做一个变换 \(t=e^{-\lambda}\),就可以得到我们常见的伽玛函数形式 \begin{equation} \label{factorial-gamma-2} n! = \int_0^{\infty} \lambda^ne^{-\lambda}d\lambda . \tag{2.11} \end{equation}

把 \eqref{factorial-gamma-1}和 \eqref{factorial-gamma-2} 式从整数\(n\) 延拓到任意实数\(x\)(包括负数)，我们就得到伽玛函数的一般形式

$$ \Gamma(x+1) = \int_0^1 (-\log t)^{x}dt = \int_0^{\infty} t^{x}e^{-t}dt .$$

1730年 欧拉把他推广得到的\(n!\)的积分形式再次写信告知了哥德巴赫，由此完美地解决了困恼哥德巴赫多年的插值问题，同时正式宣告了伽马函数在数学史的诞生，当时欧拉只有23岁。

虽然会有一些争议，有不少数学人把数学家排名中的头两把交椅划给了欧拉和高斯。欧拉和高斯都是具有超凡直觉的一流数学家，但是欧拉和高斯的风格迥异。高斯是个老狐狸，数学上非常严谨，发表结果的时候却都把思考的痕迹抹去，只留下漂亮的结果，这招致了一些数学家对高斯的批评。而欧拉的风格不同，他的做法是把最基本的东西解释得尽量清楚，讲明引导他得出结论的思路，经常通过经验直觉做大胆的猜测，他的文章中往往留下了做数学猜想的痕迹。 拉普拉斯曾说过：“读读欧拉 ,他是我们所有人的老师。”高斯的评价是：“学习欧拉的著作，乃是认识数学的最好工具。”数学家波利亚在他的名著《数学与猜想》中列举了许多欧拉做数学研究的例子，对欧拉做数学归纳和猜想的方式推崇备至。

欧拉被称为分析学的化身，在分析学中，无出其右者。欧拉的老师约翰·贝努利在给欧拉的信中这样评价欧拉的工作：“ 我介绍高等分析的时候，它还是个孩子，而你正在将它带大成人。” 希尔伯特说“分析学是无穷的交响曲”，欧拉显然是无穷分析中最出色的作曲家。欧拉二百多年前写的教科书《无穷分析引论》至今还在不断地印刷，最近也刚刚出版了中文翻译版本。布尔巴基学派的灵魂人物韦伊( Andr'{e} Weil, 1906-1998) 1979 年在 Rochester大学的一次讲演中说：“今天的学生从欧拉的《无穷分析引论》中所能得到的益处，是现代的任何一本数学教科书都比不上的。”

许多人把数学比作音乐，把欧拉称作数学界的贝多芬。因为贝多芬在两耳失聪之后继续谱写了大量著名的交响曲，而欧拉在60岁左右双目失明之后仍然以口述形式完成了几本书和 400 多篇论文，在数学上变得更加多产。 数学界从1911年开始出版《欧拉全集》，耗费了一个世纪的时间，已经出版了70余卷，25000 多页， 而这项庞大的出版任务还仍处于未完成状态。

下载 LaTeX 排版的 PDF 格式文档，请点击这里。