本文讲述一下蒙特卡洛模拟方法与定积分计算,首先从一个题目开始:设\(0\leq f(x) \leq 1\),用蒙特卡洛模拟法求定积分\(J=\int_{0}^{1}f(x)dx\)的值。
随机投点法
设\((X,Y)\)服从正方形 \(\{0\leq x \leq 1,0\leq y\leq 1\}\)上的均匀分布,则可知 \(X,Y\)分别服从[0,1]上的均匀分布,且\(X,Y\)相互独立。记事件\(A=\{Y\leq f(X)\}\),则\(A\)的概率为
$$P(A)=P(Y\leq f(X))=\int_{0}^{1}\int_{0}^{f(x)}dydx=\int_{0}^{1}f(x)dx=J$$
即定积分\(J\)的值 就是事件\(A\)出现的频率。同时,由伯努利大数定律,我们可以用重复试验中\(A\)出现的频率作为 \(p\)的估计值。即将\((X,Y)\)看成是正方形\(\{0\leq x \leq 1,0\leq y \leq 1\}\)内的随机投点,用随机点落在区域\({y\leq f(x)}\)中的频率作为定积分的近似值。这种方法就叫随机投点法,具体做法如下:
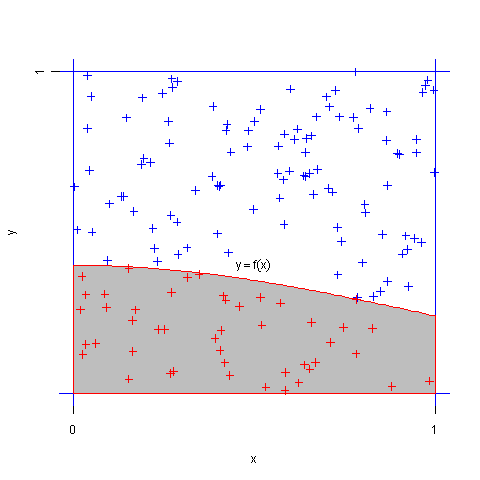
1、首先产生服从 \([0,1]\)上的均匀分布的\(2n\)个随机数( \(n \)为随机投点个数,可以取很大,如 \(n=10^4\) )并将其配对。
2、对这\(n\)对数据 \((x_i,y_i),i=1,2,...;,n\),记录满足不等式\(y_i\leq f(x_i)\)的个数,这就是事件 \(A\) 发生的频数\(\mu_n\),由此可得事件\(A\)发生的频率\(\frac{\mu_n}{n}\),则\(J\approx \frac{\mu_n} {n}\)。
举一实例,譬如要计算\(\int_{0}^{1}e^{-x^2/2}/\sqrt{2\pi}dx\),模拟次数\(n=10^4\)时,R代码如下:
n=10^4;
x=runif(n);
y=runif(n);
f=function(x)
{
exp(-x^2/2)/sqrt(2*pi)
}
mu_n=sum(y<f(x));
J=mu_n/n;
J
模拟次数 \(n=10^5\) 时,令\(n=10^5\),其余不变。
定积分\(\int_{0}^{1}e^{-x^2/2}/\sqrt{2\pi}dx\)的精确值和模拟值如下:
表1
| 精确值 | \(10^3\) |
\(10^4\) |
\(10^5\) |
\(10^6\) |
\(10^7\) |
|---|---|---|---|---|---|
| 0.3413447 | 0.342 | 0.344 | 0.34187 | 0.341539 | 0.341302 |
注:精确值用integrate(f,0,1)求得
扩展
如果你很细心,你会发现这个方法目前只适用于积分区间\([0,1]\) ,且积分函数 \(f(x)\) 在区间\([0,1]\)上的取值也位于 \([0,1]\) 内的情况。那么,对于一般区间 \([a,b]\) 上的定积分\(J'=\int_{a}^{b}g(x)dx\) 呢?一个很明显的思路,如果我们可以将 \(J'\) 与\(J\) 建立代数关系就可以了。
首先,做线性变换,令 \(y=(x-a)/(b-a)\) ,此时,
\(x=(b-a)y+a\), \(J'=(b-a)\int_{0}^{1}g[(b-a)y+a]dy\)。
进一步如果在区间\([a,b]\)上有\(c\leq g(x) \leq d \) ,令
\(f(y)=\frac{1}{d-c}{g(x)-c}=\frac{1}{d-c}{g[a+(b-a)y]-c} \),
则\(0\leq f(y) \leq 1\)。此时,可以得到\J'=\int_{a}^{b}g(x)dx=S_0J+c(b-a) \)。
其中,\(S_0=(b-a)(d-c) \), \(J=\int_{0}^{1}f(y)dy \)。
这说明,用随机投点法计算定积分方法具有普遍意义。
举一个实例,求定积分 \(J'=\int_{2}^{5}e^{-x^2/2}/\sqrt{2\pi}dx \)。
显然\(a=2,b=5\),\(c=min\{g(x)|2\leq x \leq 5\},d=max\{g(x)|2\leq x \leq 5\}\),由于\(g(x)=e^{-x^2/2}/\sqrt{2\pi}\)在 \([2,5]\)上时单调减函数,所以\(c=g(5),d=g(2)\),\(S_0=(b-a)(d-c)\)。R中代码为
a=2;
b=5;
g=function(x)
{
exp(-x^2/2)/sqrt(2*pi);
}
f=function(y)
{
(g(a+(b-a)*y)-c)/(d-c);
}
c=g(5);d=g(2);s_0=(b-a)*(d-c);
n=10^4;
x=runif(n);y=runif(n);
mu_n=sum(y<=f(x));
J=mu_n/n;
J_0=s_0*J+c*(b-a);
定积分 \(J'=\int_{2}^{5}e^{-x^2/2}/\sqrt{2\pi}dx\) 的精确值和模拟值如下:
表2
| 真实值 | \(10^3\) |
\(10^4\) |
\(10^5\) |
\(10^6\) |
\(10^7\) |
|---|---|---|---|---|---|
| 0.02274985 | 0.02332792 | 0.02311736 | 0.02262659 | 0.02284152 | 0.02278524 |
注:精确值用integrate(g,2,5)求得
平均值法
蒙特卡洛模拟法计算定积分时还有另一种方法,叫平均值法。这个原理也很简单:设随机变量 \(X\) 服从\([0,1]\)上的均匀分布,则\(Y=f(X)\)的数学期望为
$$ E(f(X))=\int_{0}^{1}f(x)dx=J $$
所以估计\(J\)的值就是估计\(f(X)\)的数学期望值。由辛钦大数定律,可以用\(f(X)\)的观察值的均值取估计\(f(X)\)的数学期望。具体做法:
先用计算机产生\(n\)个服从\([0,1]\)上均匀分布的随机数:\(x_i,i=1,2,...;,n\)。
对每一个\(x_i\) ,计算\(f(x_i)\)。
计算\(J\approx \frac{1}{n}\sum_{i=1}^{n}f(x_i)\)。
譬如,计算 \(J=\int_{0}^{1}e^{-x^2/2}/\sqrt{2\pi}dx \),R中的代码为
n=10^4;
x=runif(n);
f=function(x)
{
exp(-x^2/2)/sqrt(2*pi)
}
J=mean(f(x));
其精确值和模拟值如下:
表3
| 真实值 | \(10^3\) |
\(10^4\) |
\(10^5\) |
\(10^6\) |
\(10^7\) |
|---|---|---|---|---|---|
| 0.3413447 | 0.3405831 | 0.3410739 | 0.3414443 | 0.3414066 | 0.3413366 |
平均值法与随机投点法类似可以进行扩展,这里不再赘述。
结论
用蒙特卡洛模拟法计算定积分具有普遍意义。蒙特卡洛模拟方法为我们提供了一个看待世界的新思路,即一个不具随机性的事件可以通过一定的方法用随机事件来模拟或逼近。

发表/查看评论