本文作者:姜晓东,博士毕业于上海交通大学,目前任教于湖南师范大学医学院,专业神经毒理学。
缘起
谈起测量灯泡体积,大家一定记得那个耳熟能详的故事。相传爱迪生发明灯泡的时候,让他的助手阿普顿测量一个灯泡的体积。助手用尺子进行了反复测量,并列出很很多公式,算了很久还没有算出来。爱迪生见罢,拿起那只灯泡,注满水后用量桶测出了体积。助手看了之后幡然醒悟,爱迪生主角光环大亮,随后开示了“不要钻牛角尖”、“时间就是生命”等人生哲理。
每当想起这个故事,不免让人产生很多疑问。爱迪生的这个助手究竟用什么方法来计算体积,为什么这么费时?爱迪生看到后为什么没有直接口头提醒,反而以行动让助手难堪?灯泡注水倒出去后,里面残余液体会不会影响后续的实验?
最近研究R语言的数学计算时,发现R中有非常方便的数值积分函数,可以很快进行求体积等计算。于是上面的那个典故及疑问便涌上心头,索性查清楚文献,做一个了断。
阿普顿其人
在有些版本的典故中有提到,爱迪生的那个助手名为阿普顿(Francis R. Upton)。在维基百科上也有这个人的词条。维基百科上的照片是这样子的,上面有他的签名。
阿普顿从小就受到良好的教育,从美国的重点高中Phillips Academy毕业后,进入Bowdoin College攻读本科学位。之后进入普林斯顿大学,拿到硕士学位。毕业后,游学欧洲,在柏林度过了自己的academic year(美国的很多大学生在毕业后一年并不直接找工作,而是进行旅游、访学等活动了解社会,之后再决定自己的下一步,这一年也称为gap year),并在当时的物理学大牛Hermann von Helmholtz手下工作,参与了数学角度分析电路动力学的课程。
当时爱迪生正处于研制电灯的瓶颈期,爱迪生虽然惊才艳艳,但毕竟是自学成才,虽然有很多巧妙的想法,但是实际执行中却饶不开理论物理和高等数学的障碍,于是他向Helmholtz求援,要求推荐一名助手。Helmholtz便推荐阿普顿作为爱迪生的助手。
阿普顿到任后,给予爱迪生很大的帮助。爱迪生公司供电系统中很多问题的解决都有赖于阿普顿,这些数学分析可以从现存遗留下来的爱迪生笔记中找到。在电灯的发明上,阿普顿也给爱迪生很多建议,缩小范围,优化加速了寻找灯丝材料的步伐,在阿普顿工作的第二年,电灯问世。
爱迪生发现阿普顿不仅理论高超,而且易于相处,富有才干。二人合作愉悦,很多重要发明都有二者的讨论。电灯问世后,爱迪生成立了爱迪生灯泡厂,由阿普顿出任总经理。在摩根家族的支持和运作下,爱迪生的公司逐步发展成了今天的通用电气公司(GE),汽车、飞机、核磁共振,领域广泛。
阿普顿一生在理论和实践上都有所贡献,其去世后,纽约时报全文对其报道。他的母校普林斯顿大学也设立以其名字命名的奖学金,以兹纪念。
亲历者版本的测量灯泡故事
爱迪生让阿普顿量灯泡的故事有很多版本,是非难辨。但是当时在场的第三人,爱迪人的另外一个助手Francis Jehl,在其回忆录中真实描述了这个故事。
“I was once with Mr Upton calculating some tables he had put me on, when Mr Edison appeared with a glass bulb having a pear-shaped appearance in his hand. It was the kind we were going to use for our lamp experiments; and Mr Edison asked Mr Upton to please calculate its cubical content in centimetres. Now Mr Upton was a very able mathematician, who after he finished his studies at Princeton went to Germany and got his final gloss under the great master Helmholtz. Whatever he did and worked on was executed in a purely mathematical manner and any Wrangler at Cambridge would have been delighted to see him juggle with integral and differential equations with a dexterity that was surprising. He drew the shape of the bulb exactly on paper, and got the equation of its lines with which he was going to calculate its contents, when Mr Edison again appeared and asked him what it was. He showed Mr Edison the work he had already done on the subject and told him he would very soon finish calculating it. “Why,” said Edison, “I would simply take that bulb and fill it with mercury and weigh it; and from the weight of the mercury and its specific gravity, I’ll get it in five minutes, and use a lot less mental energy than is necessary in such a fatiguing operation.”
“我有一次正和阿普顿先生计算一些他拿过来的数据表。这时,爱迪生先生出现了。他手里拿着一个梨子形状的灯泡,这正是我们准备进行电灯实验的那种型号。爱迪生先生请求阿普顿先生计算一下灯泡的容积是多少立方厘米。阿普顿先生现在已经是一名非常出色的数学家了,他曾在普林斯顿大学完成学业,又去过德国,在大牛 Helmholtz 那里更近层楼,数学方面已经很厉害了。他在以纯数学的方式解决问题的时候,灵活熟练地在微积分方程间闪辗腾挪,哪怕是任何一名剑桥大学毕业的牛仔都会羡慕惊艳。阿普顿先生首先在纸上准确第勾勒出灯泡的形状。然后他用方程拟合好了轮廓曲线,正要根据这些结果计算体积的时候,爱迪生先生就回来询问结果了。阿普顿先生展示了已经做的,并告诉他将很快完成计算。’为什么?’爱迪生说,‘我会简单地在灯泡中注入汞并称重,根据汞的重量及其密度,5分钟就会得到灯泡的体积。比起这项累人的计算,要省下不少的脑力。’”
从这份亲历者的描述中,我们了解到爱迪分并非有意刁难阿普顿,而仅仅是工作上常规的讨论,之后也没有发表人生哲理感言。爱迪生的方法是向灯泡中注入汞,而不是流传版本中所说的水。这样由于汞的高表面张力,及与玻璃的不浸润。再倒走后没有残留,也就不影响后续实验了。从另一个方面来说,爱迪生实验室非常有钱。
文章前提到的疑问基本解决了,最后剩下的疑问是阿普顿是怎么计算体积的?为什么耗时?
阿普顿的计算方法
爱迪生公司生产的灯泡,现在在网上仍有仿古版本售卖,eBay上的这张图展示了其中一些型号的碳丝灯:

阿普顿之所以进行复杂计算,做是由于灯泡形状不规则造成的,没有现成通用的公式。从上文中,我们知道阿普顿的计算方法由3步组成:
- 勾勒灯泡轮廓曲线;
- 对曲线进行方程拟合;
- 根据曲线方程,进行积分,求体积。
在100年前,阿普顿没有计算机,不能编程,更不能用R语言,完成这些工作全靠手工计算。需要在精度和算法间权衡,需要很多复杂的技巧来简化运算。能在短时间内快速准确地完成这些计算已经是非常了不起了。
今天,有R这把利器在手,让我们沿着阿普顿先生的脚步,再走一下当年的路。
R语言计算灯泡体积
1. 勾勒灯泡轮廓曲线
我们有了灯泡的照片,其实就已经有了灯泡的轮廓曲线,所要做的仅仅是把像素尺度和实际距离换算一下就好了。
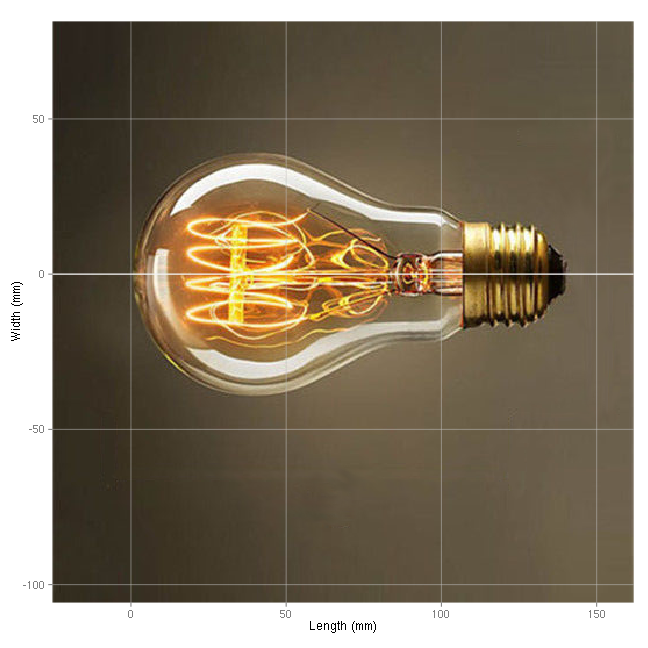
阿普顿当时测量的灯泡是梨子形状的,我从上面的图片中挑选了一个形状最接近的,型号是A19。商家细心地在网站上标注了灯泡的长度是140mm。这样就方便进行图像像素和实际尺寸的换算。
根据灯泡是实际长度,与像素进行换算,将灯泡顶点作为原点,在R中写好换算代码如下:
realx = function(x){(x-68)*140/(442-68)}
realy = function(y){(y-283)*140/(442-68)}
至此,第一步工作就完成了。
当然我们也可以继续用R语言中的ggplot2包进行绘图,将灯泡在新坐标中画出来,这一步不是必需的。
library(png)
library(ggplot2)
mypic = readPNG("pics/A19.png")
myaddr = data.frame(x=rep(1:500,500), y=rep(1:500,each=500))
myaddr$cols = apply(myaddr, 1, function(x){
rgb(mypic[x[1],x[2],1],
mypic[x[1],x[2],2],
mypic[x[1],x[2],3])})
myaddr$x = realx(myaddr$x)
myaddr$y = realy(myaddr$y)
pic = ggplot(myaddr) + geom_raster(aes(x,y,fill=cols)) +
geom_hline(aes(yintercept=tk), colour="grey",alpha=0.5,
data=data.frame(tk=c(-100,-50,0,50))) +
geom_vline(aes(xintercept=tk), colour="grey",alpha=0.5,
data=data.frame(tk=c(0,50,100,150))) +
geom_hline(yintercept=0,colour="white") +
scale_fill_identity() + coord_fixed() +
scale_x_continuous(expand=c(0,0)) +
scale_y_continuous(expand=c(0,0)) +
labs(x="Length (mm)", y="Width (mm)")
print(pic)
2. 对曲线进行方程拟合
我们首先用gimp对原始照片中灯泡的边缘选取一些点采样坐标,并转化为真实坐标。
mypoints = data.frame(y = c(283, 304, 320, 337, 354, 374, 388, 385, 368, 344, 341, 339, 329),
x = c( 68, 70, 74, 82, 95, 120, 168, 202, 240, 289, 311, 334, 352))
mypoints$x = realx(mypoints$x)
mypoints$y = realy(mypoints$y)
mypoints
## y x
## 1 0.000 0.0000
## 2 7.861 0.7487
## 3 13.850 2.2460
## 4 20.214 5.2406
## 5 26.578 10.1070
## 6 34.064 19.4652
## 7 39.305 37.4332
## 8 38.182 50.1604
## 9 31.818 64.3850
## 10 22.834 82.7273
## 11 21.711 90.9626
## 12 20.963 99.5722
## 13 17.219 106.3102
对采样点进行三次样条插值,对轮廓进行曲线拟合:
library(splines)
myfx = interpSpline(mypoints$x,mypoints$y)
整个第二部分的工作,曲线拟合已经做完了,整个第二部分就只需要一行语句负责计算!
方程曲线保存在自变量myfx中。
曲线采样分段拟合,每段采样三次多项式表示:
y = A + Bx + Cx2 + Dx3 , x[i] ≤ x < x[i+1]
后续的编程中,不必具体知道这些系数究竟是多少。非要查看的话,在自定义变量myfx中,可以查看,这些方程的系数分别是:
tmpdf = as.data.frame(myfx$coefficients); tmpdf$V5=(myfx$knots);
names(tmpdf) <- c("A", "B", "C", "D", "x[i]"); kable(tmpdf, "html");
| A | B | C | D | x[i] |
|---|---|---|---|---|
| 0.000 | 11.5973 | 0.0000 | -1.9577 | 0.0000 |
| 7.861 | 8.3054 | -4.3970 | 1.0162 | 0.7487 |
| 13.850 | 1.9730 | 0.1678 | -0.0391 | 2.2460 |
| 20.214 | 1.9265 | -0.1834 | 0.0116 | 5.2406 |
| 26.578 | 0.9625 | -0.0147 | -0.0003 | 10.1070 |
| 34.064 | 0.6130 | -0.0226 | 0.0003 | 19.4652 |
| 39.305 | 0.0554 | -0.0084 | -0.0002 | 37.4332 |
| 38.182 | -0.2684 | -0.0170 | 0.0003 | 50.1604 |
| 31.818 | -0.5630 | -0.0037 | 0.0004 | 64.3850 |
| 22.834 | -0.2761 | 0.0193 | -0.0003 | 82.7273 |
| 21.711 | -0.0160 | 0.0123 | -0.0024 | 90.9626 |
| 20.963 | -0.3344 | -0.0492 | 0.0024 | 99.5722 |
| 17.219 | -0.6661 | 0.0000 | 0.0000 | 106.3102 |
也可以把这些点,和拟合好的曲线画在图上,看看效果:
mysmooth = as.data.frame(predict(myfx, x=seq(0, max(mypoints$x), length.out=100)))
pic = pic + geom_line(aes(x,y), size=1.3, colour="yellow", data=mysmooth) +
geom_point(aes(x,y), shape=13,size=5,colour="white",data=mypoints) +
annotate("text",x=20,y=-60,label="V==integral(pi*f(x)^2*dx,a,b)",
size=8, colour="white", parse=TRUE, hjust=0) +
annotate("text",x=20,y=-85,label="f(x)=Spline of Points",
size=6, colour="white", hjust=0)
print(pic)

可以看到,曲线完美拟合灯泡的轮廓。
3. 根据曲线方程,进行积分,求体积。
V = integrate(function(x){pi*(predict(myfx,x)$y)^2}, 0, max(mypoints$x))
print(V)
## 311680 with absolute error < 34
我们得到结果,灯泡的体积是 3.1168 × 105 mm3 ,按照爱迪生的厘米单位要求,是311.68 cm3 。上述代码中,真正用于计算的代码只有寥寥几行,阿普顿先生勾勒完曲线后,只要花费几分钟输入R代码,马上就可以在爱迪生先生回来前得到结果了。
结尾
100年后的今天,我们有了R语言,不再需要懂复杂的技巧和高深的理论,就可以轻松完成这些工作。不过,却再也没有微积分闪耀在稿纸上的灵动,再也没有剑桥牛仔投向阿普顿的热切眼神了。我们只能在文献的字里行间,隐约感觉到折射出来的人性光辉,在心底投以满满的敬意。
参考文献
- 维基百科, Francis Robbins Upton, http://en.wikipedia.org/wiki/Francis_Robbins_Upton
- J J O’Connor and E F Robertson, Francis Robbins Upton, http://www-history.mcs.st-andrews.ac.uk/Biographies/Upton.html

发表/查看评论