用过底层语言做计算的人转入R语言的时候一般都会觉得R语言的运算太慢，这是一个常见的对R的误解或者对R的设计的不理解。在二三十年前Chambers等一群人在贝尔实验室设计S语言之前，统计计算主要是通过那些底层语言实现的，典型的如Fortran。当时有一个基于Fortran的统计分析库，用它的麻烦就在于无论做什么样的数据分析，都涉及到一大摞繁琐的底层代码，这让数据分析变得很没劲，统计学家有统计学家的事情，天天陷在计算机程序代码中也不是个办法，要摆脱底层语言，那就只能设计高层语言了。有所得必有所失，众所周知，高层语言一般来说比底层语言低效，但对用户来说更友好。举个简单的例子，用C语言计算均值时，我们得对一个向量（数组）从头循环到尾把每个值累加起来，得到总和，然后除以向量的长度，而均值在统计当中简直是再家常便饭不过了，要是每次都要来这么个循环，大家也都甭干活儿了，天天写循环好了。

前两天COS论坛上有个帖子提到“R语言的执行效率问题”，大意如下：

有120000行数据，用perl写成12万行R命令做t.test，然后执行，大概几分钟就算完了。如果只用R语言，把所有数据先读入，然后用循环，每一行做t.test，花了几个小时，到现在还没有算完。这说明一个问题，在R里执行单行命令要比用循环快，涉及到循环的问题，最好写成单行命令执行。

我不清楚作者是如何写这“12万行”R命令的，本文假设是把t.test(dat[i, ]), i = 1, 2, ..., 120000写入一个文件，然后用source()执行之。面对这样一个问题，我们有若干种改进计算的可能性。首先我们看“硬”写入程序代码的方法：

## 为了使计算可重复，设定随机数种子
set.seed(123)
## 生成数据，随机数，120000行 x 100列矩阵
dat = matrix(rnorm(120000 * 100), 120000)
nr = nrow(dat)
nc = ncol(dat)
## 六种方法的P值向量
p1 = p2 = p3 = p4 = p5 = p6 = numeric(nr)

## via source()
f = file("test.t")
writeLines(sprintf("p1[%d] = t.test(dat[%d, ])$p.value",
    seq(nr), seq(nr)), f)
system.time({
    source(f)
})
#   user  system elapsed
#  95.36    0.19   95.86
close(f)
unlink("test.t")

1、向量式计算：apply()以及*apply()

当我们需要对矩阵的行或者列逐一计算时，apply()系列函数可能会提高效率。本例是对矩阵的行做t检验，那么可以这样计算：

## via apply()
system.time({
    p2 = apply(dat, 1, function(x) {
        t.test(x)$p.value
    })
})
#   user  system elapsed
#  63.12    0.06   63.50
identical(p1, p2)
# [1] TRUE

结果比第一种方法快了大约半分钟，而且计算结果完全一样。apply()本质上仍然是循环，但它在某些情况下比直接用显式循环要快：

## via for-loop
system.time({
    for (i in seq(nr)) p3[i] = t.test(dat[i, ])$p.value
})
#   user  system elapsed
#  69.88    0.03   70.05
identical(p2, p3)
# [1] TRUE

不过apply()系列函数在提高运算速度上优势并不会太明显，提倡用它的原因是它和统计中的矩阵运算相似，可以简化代码，相比起$\sum_{i=1}^n x_i/n$，我们可能更愿意看$\bar{x}$这样的表达式。很多R内置函数都是用底层语言写的，我们需要做的就是把一个对象作为整体传给函数去做计算，而不要自行把对象分解为一个个小部分计算，这个例子可能更能体现向量式计算的思想：

system.time(apply(dat, 1, mean))
#   user  system elapsed
#   5.28    0.04    5.25
system.time({
    x = numeric(nr)
    for (i in 1:nr) x[i] = mean(dat[i, ])
})
#   user  system elapsed
#   4.44    0.02    4.42
system.time(rowMeans(dat))
#   user  system elapsed
#   0.11    0.00    0.13

2、明确计算的目的

很多情况下，R函数返回的不仅仅是一个数字作为结果，而是会得到一系列诸如统计量、P值、各种系数等对象，在我们调用R函数之前如果能想清楚我们究竟需要什么，也许对计算的速度提升有帮助。比如本例中，也许我们仅需要12万个双边P值，其它数字我们都用不着，那么可以考虑“手工”计算P值：

## "hand" calculation in R
system.time({
    p4 = 2 * pt(apply(dat, 1, function(x, mu = 0) -abs((mean(x) -
        mu)/sqrt(var(x)/nc))), nc - 1)
})
#   user  system elapsed
#  15.97    0.07   16.08
identical(p3, p4)
# [1] TRUE

上面的计算更“纯净”，所以计算速度有了本质的提升，而且计算的结果和前面毫无差异。在做计算之前，人的脑子多思考一分钟，也许计算机的“脑子”会少转一个小时。

3、把四则运算交给底层语言

R是高层语言，把它拿来做简单的四则运算是很不划算的，而且容易导致程序低效。加加减减的活儿是C和Fortran等底层语言的强项，所以可以交给它们去做。以下我们用一段C程序来计算t统计量，然后用R CMD SHLIB将它编译为dll（Windows）或so（Linux）文件，并加载到R中，用.C()调用，最终用R函数pt()计算P值：

## "hand" calculation in C for t-statistic
writeLines("#include <math.h>

void calc_tstat(double *x, int *nr, int *nc, double *mu, double *tstat)
{
    int i, j;
    double sum = 0.0, sum2 = 0.0, mean, var;
    for (i = 0; i < *nr; i++) {
        for (j = 0; j < *nc; j++) {
            sum += x[i + j * *nr];
        }
        mean = sum / (double) *nc;
        sum = 0.0;
        for (j = 0; j < *nc; j++) {
            sum2 += (x[i + j * *nr] - mean) * (x[i + j * *nr] - mean);
        }
        var = sum2 / (double) (*nc - 1);
        sum2 = 0.0;
        tstat[i] = (mean - *mu) / sqrt(var / (*nc - 1));
    }
}", "calc_tstat.c")
system("R CMD SHLIB calc_tstat.c")
dyn.load(sprintf("calc_tstat%s", .Platform$dynlib.ext))
system.time({
    p5 = 2 * pt(-abs(.C("calc_tstat", as.double(dat), nr, nc,
        0, double(nrow(dat)))[[5]]), nc - 1)
})
#   user  system elapsed
#   0.86    0.06    0.92
dyn.unload(sprintf("calc_tstat%s", .Platform$dynlib.ext))

因为R可以用system()调用系统命令，所以整个过程全都可以用R完成，Windows用户需要安装Rtools并设置系统环境变量PATH才能使用R CMD SHLIB。

更进一步，因为R自身的一些C程序也是可供用户的C程序调用的，所以我们可以把整个P值的计算过程全都扔进C代码中，一步完成：

## "hand" calculation in C calling Rmath.h
writeLines("#include <Rmath.h>
void calc_pvalue(double *x, int *nr, int *nc, double *mu, double *pval)
{
    int i, j;
    double sum = 0.0, sum2 = 0.0, mean, var;
    for (i = 0; i < *nr; i++) {
        for (j = 0; j < *nc; j++) {
            sum += x[i + j * *nr];
        }
        mean = sum / (double) *nc;
        sum = 0.0;
        for (j = 0; j < *nc; j++) {
            sum2 += (x[i + j * *nr] - mean) * (x[i + j * *nr] - mean);
        }
        var = sum2 / (double) (*nc - 1);
        sum2 = 0.0;
        pval[i] = 2 * pt(-fabs((mean - *mu) / sqrt(var / (*nc - 1))),
                      (double) (*nc - 1), 1, 0);
    }
}", "calc_pvalue.c")
system("R CMD SHLIB calc_pvalue.c")
dyn.load(sprintf("calc_pvalue%s", .Platform$dynlib.ext))
system.time({
    p6 = .C("calc_pvalue", as.double(dat), nr, nc, as.double(0),
        double(nrow(dat)))[[5]]
})
#   user  system elapsed
#   0.83    0.07    0.91
dyn.unload(sprintf("calc_pvalue%s", .Platform$dynlib.ext))

头文件Rmath.h的引入使得我们可以调用很多基于C程序的R函数，详情参考手册Writing R Extensions。通过C计算出来的P值和前面用R算的略有差异，下面画出p6 - p1 vs p1以及p6 - p5 vs p5的图：

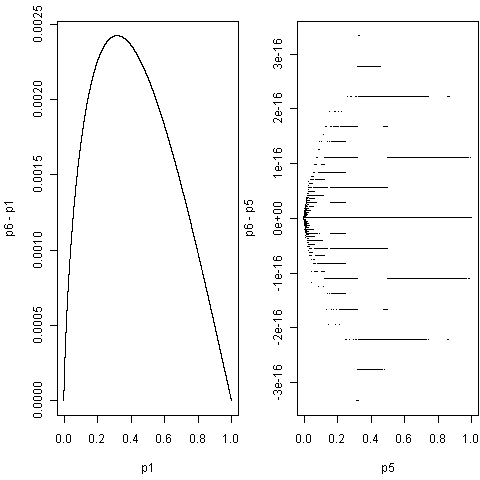
P值的差异

导致差异的原因此处不细究，感兴趣的读者可以帮忙检查一下。

小结

1. 若你熟悉底层语言，计算又不太复杂，那么可用底层语言写，然后用R调之；
2. 否则把R对象当做整体去计算，能做x + 1就不要做for (i in length(x)) x[i] + 1
3. 不要低估R core们的编程水平，他们已经做了很多工作让用户脱离底层编程

注：本文中的运算时间可能不可重复，这与计算机所处的状态有关，但大体来说，运算速度的快慢是可以肯定的。本文仅仅是关于统计计算的一个微小的例子，以后若有更好的例子，可能会更新本文；也欢迎各位提供更多示例。