因果推断简介之一：从 Yule-Simpson’s Paradox 讲起

在国内的时候，向别人介绍自己是研究因果推断（causal inference）的，多半的反应是：什么？统计还能研究因果？这确实是一个问题：统计研究因果，能，还是不能？直接给出回答，比较冒险；如果有可能，我需要花一些篇幅来阐述这个问题。

目前市面上能够买到的相关教科书仅有 2011 年图灵奖得主 Judea Pearl 的 Causality: Models, Reasoning, and Inference。Harvard 的统计学家 Donald Rubin 和 计量经济学家 Guido Imbens 合著的教科书历时多年仍尚未完成；Harvard 的流行病学家 James Robins 和他的同事也在写一本因果推断的教科书，本书目前只完成了第一部分，还未出版（见此处）。我本人学习因果推断是从 Judea Pearl 的教科书入手的，不过这本书晦涩难懂，实在不适合作为入门的教科书。Donald Rubin 对 Judea Pearl 提出的因果图模型（causal diagram）非常反对，他的教科书中杜绝使用因果图模型。我本人虽然脑中习惯用图模型进行思考，但是还是更偏好 Donald Rubin 的风格，因为这对于入门者，可能更容易。不过这一节，先从一个例子出发，不引进新的统计符号和概念。

天才的高斯在研究天文学时，首次引进了最大似然和最小二乘的思想，并且导出了正态分布（或称高斯分布）。其中最大似然有些争议，比如 Arthur Dempster 教授说，其实高斯那里的似然，有贝叶斯或者信仰推断（fiducial inference）的成分。高斯那里的“统计”是关于 “误差”的理论 ，因为他研究的对象是“物理模型”加“随机误差”。大约在 100 多年前，Francis Galton 研究了父母身高和子女身高的“关系”，提出了“（向均值）回归”的概念。众所周知，他用的是线性回归模型。此时的模型不再是严格意义的“物理模型”，而是“统计模型” — 用于刻画变量之间的关系，而不一定是物理机制。之后，Karl Pearson 提出了“相关系数”（correlation coefficient）。后世研究的统计，大多是关于 “相关关系”的理论。 但是关于 “因果关系” 的统计理论，非常稀少。据 Judea Pearl 说，Karl Pearson 明确地反对用统计研究因果关系；有意思的是，后来因果推断为数不多的重要文章（如 Rosenbaum and Rubin 1983; Pearl 1995）都发表在由 Karl Pearson 创刊的 Biometrika 上。下面讲到的悖论，可以说是困扰统计的根本问题，我学习因果推断便是由此入门的。

在高维列联表分析中， 有一个很有名的例子，叫做 Yule-Simpson’s Paradox。有文献称，Karl Pearson 很早就发现了这个悖论 — 也许这正是他反对统计因果推断的原因。此悖论表明，存在如下的可能性：$X$ 和 $Y$ 在边缘上正相关；但是给定另外一个变量 $Z$ 后，在 $Z$ 的每一个水平上，$X$ 和 $Y$ 都负相关。Table 1 是一个数值的例子，取自 Pearl (2000)。

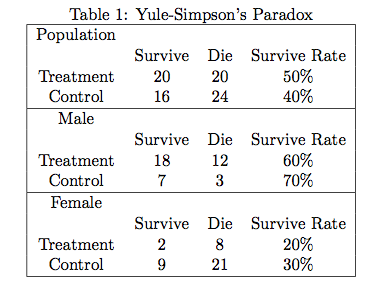
Table 1 中，第一个表是整个人群的数据：接受处理和对照的人都是 40 人，处理有较高的存活率，因此处理对整个人群有“正作用”。第二个表和第三个表是将整个人群用性别分层得到的，因为第一个表的四个格子数，分别是下面两个表对应格子数的和： $$20 = 18+2, 20 = 12+8, 16 = 7+9, 24 = 3+21.$$ 奇怪的是，处理对男性有“负作用”，对女性也有“负作用”。一个处理对男性和女性都有“负作用”，但是他对整个人群却有“正作用”：悖论产生了！

有人可能会认为这种现象是由于随机性或者小样本的误差导致的。但是这个现象与样本量无关，与统计的误差也无关。比如，将上面的每个格子数乘以一个巨大的正数，上面的悖论依然存在。

纯数学的角度，上面的悖论可以写成初等数学 $ \frac{a}{b} < \frac{c}{d}, \frac{a’}{b’} < \frac{c’}{d’} , \frac{a  + a’}{b + b’} > \frac{c + c’}{d + d’} $；这并无新奇之处。但是在统计上，这具有重要的意义 — 变量之间的相关关系可以完全的被第三个变量“扭曲”。更严重的问题是，我们的收集的数据可能存在局限性，忽略潜在的“第三个变量”可能改变已有的结论，而我们常常却一无所知。鉴于 Yule-Simpson 悖论的潜在可能，不少人认为，统计不可能用来研究因果关系。

上面的例子是人工构造的，在现实中，也存在不少的实例正是 Yule-Simpson’s Paradox。比如，UC Berkeley 的著名统计学家 Peter Bickel 教授 1975 年在 Science 上发表文章，报告了 Berkeley 研究生院男女录取率的差异。他发现，总体上，男性的录取率高于女性，然而按照专业分层后，女性的录取率却高于男性 (Bickel 等 1975)。在流行病学的教科书 (如 Rothman 等 2008) 中，都会讲到“混杂偏倚”（confounding bias），其实就是 Yule-Simpson’s Paradox，书中列举了很多流行病学的实际例子。

由于有 Yule-Simpson’s Paradox 的存在，观察性研究中很难得到有关因果的结论，除非加上很强的假定，这在后面会谈到。比如，一个很经典的问题：吸烟是否导致肺癌？由于我们不可能对人群是否吸烟做随机化试验，我们得到的数据都是观察性的数据：即吸烟和肺癌之间的相关性 （正如 Table 1 的合并表）。此时，即使我们得到了吸烟与肺癌正相关，也不能断言“吸烟导致肺癌”。这是因为可能存在一些未观测的因素，他既影响个体是否吸烟，同时影响个体是否得癌症。比如，某些基因可能使得人更容易吸烟，同时容易得肺癌；存在这样基因的人不吸烟，也同样得肺癌。此时，吸烟和肺癌之间相关，却没有因果作用。

相反的，我们知道放射性物质对人体的健康有很大的伤害，但是铀矿的工人平均寿命却不比常人短；这是流行病学中有名的“健康工人效应”（healthy worker effect）。这样一来，似乎是说铀矿工作对健康没有影响。但是，事实上，铀矿的工人通常都是身强力壮的人，不在铀矿工作寿命会更长。此时，在铀矿工作与否与寿命不相关，但是放射性物质对人的健康是有因果作用的。

这里举了一个悖论，但没有深入的阐释原因。阐释清楚这个问题的根本原因，其实就讲清楚了什么是因果推断。这在后面会讲到。作为结束，留下如下思考的问题：

1. Table 1 中，处理组和对照组中，男性的比例分别为多少？这对悖论的产生有什么样的影响？反过来考虑处理的“分配机制”（assignment mechanism），计算 $ P(\text{Treatment} \mid \text{Male})$ 和 $P(\text{Treatment} \mid \text{Female})$。
2. 假如 $(X, Y, Z) $ 服从三元正态分布，$X$ 和 $Y$  正相关，$Y$ 和 $Z$ 正相关，那么 $X$ 和 $Z$ 是否正相关？（北京大学概率统计系 09 年《应用多元统计分析》期末第一题）
3. 流行病学的教科书常常会讲各种悖论，比如混杂偏倚 （confounding bias）和入院率偏倚（Berkson’s bias）等，本质上是否与因果推断有关？
4. 计量经济学中的“内生性”（endogeneity）怎么定义？它和 Yule-Simpson 悖论有什么联系？

参考文献：

1. Bickel, P. J. and Hammel, E. A. and O’Connell, J. W. (1975) Sex bias in graduate admissions: Data from Berkeley. Science, 187, 398-404.
2. Pearl, J. (2000) Causality: models, reasoning, and inference. Cambridge University Press。
3. Rosenbaum, P.R. and Rubin, D.B. (1983) The central role of the propensity score in observational studies for causal effects. Biometrika, 70, 41-55.
4. Rothman, K., Greenland, S. and Lash, T. L.  (2008) Modern Epidemiology. Lippincott Williams & Wilkins.